
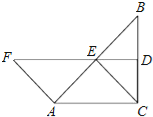
【题目】如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于D,交AB于E,F在DE上,且AF=CE=AE.
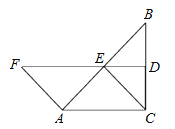
(1)说明四边形ACEF是平行四边形;
(2)当∠B满足什么条件时,四边形ACEF是菱形,并说明理由.
【答案】(1)说明见解析;(2)当∠B=30°时,四边形ACEF是菱形.理由见解析.
【解析】
试题(1)证明△AEC≌△EAF,即可得到EF=CA,根据两组对边分别相等的四边形是平行四边形即可判断;
(2)当∠B=30°时,四边形ACEF是菱形.根据直角三角形的性质,即可证得AC=EC,根据菱形的定义即可判断.
(1)证明:由题意知∠FDC=∠DCA=90°,
∴EF∥CA,
∴∠FEA=∠CAE,
∵AF=CE=AE,
∴∠F=∠FEA=∠CAE=∠ECA.
在△AEC和△EAF中,
∵
∴△EAF≌△AEC(AAS),
∴EF=CA,
∴四边形ACEF是平行四边形.
(2)解:当∠B=30°时,四边形ACEF是菱形.
理由如下:∵∠B=30°,∠ACB=90°,
∴AC=![]() AB,
AB,
∵DE垂直平分BC,
∴∠BDE=90°
∴∠BDE=∠ACB
∴ED∥AC
又∵BD=DC
∴DE是△ABC的中位线,
∴E是AB的中点,
∴BE=CE=AE,
又∵AE=CE,
∴AE=CE=![]() AB,
AB,
又∵AC=![]() AB,
AB,
∴AC=CE,
∴四边形ACEF是菱形.


科目:初中数学 来源: 题型:
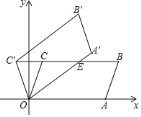
【题目】如图,在平面直角坐标系![]() 中,平行四边形
中,平行四边形![]() 的顶点
的顶点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,将平行四边形
,将平行四边形![]() 绕点
绕点![]() 逆时针方向旋转得到平行四边形
逆时针方向旋转得到平行四边形![]() ,当点
,当点![]() 落在
落在![]() 的延长线上时,线段
的延长线上时,线段![]() 交
交![]() 于点
于点![]() ,则线段
,则线段![]() 的长度为________.
的长度为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有两个纸箱,每个纸箱内各装有4个材质、大小都相同的乒乓球,其中一个纸箱内4个小球上分别写有1、2、3、4这4个数,另一个纸箱内4个小球上分别写有5、6、7、8这4个数,甲、乙两人商定了一个游戏,规则是:从这两个纸箱中各随机摸出一个小球,然后把两个小球上的数字相乘,若得到的积是2的倍数,则甲得1分,若得到积是3的倍数,则乙得2分.完成一次游戏后,将球分别放回各自的纸箱,摇匀后进行下一次游戏,最后得分高者胜出.。
(1)请你通过列表(或树状图)分别计算乘积是2的倍数和3的倍数的概率;
(2)你认为这个游戏公平吗?为什么?若你认为不公平,请你修改得分规则,使游戏对双方公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
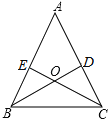
【题目】如图,△ABC的两条高BD、CE相交于点O 且OB=OC.则下列结论:
①△BEC≌△CDB;
②△ABC是等腰三角形;
③AE=AD;
④点O在∠BAC的平分线上,
其中正确的有_____.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加快“智慧校园”建设,某市准备为试点学校采购一批![]() 两种型号的一体机,经过市场调查发现,每套
两种型号的一体机,经过市场调查发现,每套![]() 型一体机的价格比每套
型一体机的价格比每套![]() 型一体机的价格多
型一体机的价格多![]() 万元,且用
万元,且用![]() 万元恰好能购买
万元恰好能购买![]() 套
套![]() 型一体机和
型一体机和![]() 套
套![]() 型一体机.
型一体机.
(1)列二元一次方程组解决问题:求每套![]() 型和
型和![]() 型一体机的价格各是多少万元?
型一体机的价格各是多少万元?
(2)由于需要,决定再次采购![]() 型和
型和![]() 型一体机共
型一体机共![]() 套,此时每套
套,此时每套![]() 型体机的价格比原来上涨
型体机的价格比原来上涨![]() ,每套
,每套![]() 型一体机的价格不变.设再次采购
型一体机的价格不变.设再次采购![]() 型一体机
型一体机![]() 套,那么该市至少还需要投入多少万元?
套,那么该市至少还需要投入多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
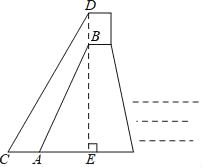
【题目】我国南水北调中线工程的起点是丹江水库,按照工程计划,需对原水库大坝进行混凝土培厚加高,使坝高由原来的162米增加到176.6米,以抬高蓄水位.如图是某一段坝体加高工程的截面示意图,其中原坝体的高为BE,背水坡坡角∠BAE=68°,新坝体的高为DE,背水坡CD的坡度为![]() :1.求工程完工后背水坡底端水平方向增加的宽度AC.(结果精确到0.1米.参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.50,
:1.求工程完工后背水坡底端水平方向增加的宽度AC.(结果精确到0.1米.参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.50,![]() ≈1.73).
≈1.73).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com