
【题目】如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高,连接EF交AD于G,下列结论:①AD垂直平分EF;②EF垂直平分AD;③AD平分∠EDF;④当∠BAC为60°时,△AEF是等边三角形,其中正确的结论的个数为( )
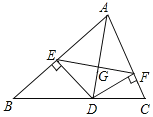
A.2B.3C.4D.1
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】苏果超市用5000元购进一批新品种的苹果进行试销,由于试销状况良好,超市又调拨11000元资金购进该种苹果,但这次的进价比试销时每千克多了0.5元,购进苹果的数量是试销时的2倍。
(1)试销时该品种苹果的进价是每千克多少元?
(2)如果超市将该品种的苹果按每千克7元定价出售,当大部分苹果售出后,余下的400千克按定价的七折售完,那么超市在这两次苹果销售中共盈利多少元?(7分)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是△ABC和△ADC的公共边,下列条件中不能判定△ABC≌△ADC的是( )
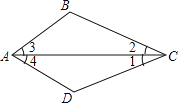
A.AB=AD,∠2=∠1
B.AB=AD,∠3=∠4
C.∠2=∠1,∠3=∠4
D.∠2=∠1,∠B=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰直角△ABC中,∠ACB=90°,P是线段BC上一动点(与点B、C不重合),连接AP,延长BC至点Q,使得CQ=CP,过点Q作QH⊥AP于点H,交AB于点M.
(1)当AP平分∠BAC时,试说明AM=AN.
(2)若∠PAC=m,求∠AMQ的大小(用含m的式子表示).
(3)用等式表示线段MB与PQ之间的数量关系,并证明.
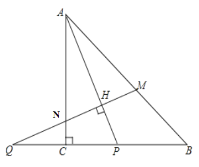
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后解答问题:
分解因式:x3+3x2-4.
解答:把x=1代入多项式x3+3x2-4,发现此多项式的值为0,由此确定多项式x3+3x2-4中有因式(x-1),于是可设x3+3x2-4=(x-1)(x2+mx+n),分别求出m,n的值,再代入x3+3x2-4=(x-1)(x2+mx+n),就容易分解多项式x3+3x2-4.这种分解因式的方法叫“试根法”.
(1)求上述式子中m,n的值;
(2)请你用“试根法”分解因式:x3+x2-16x-16.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=2,AD=4,动点E在边BC上,与点B、C不重合,过点A作DE的垂线,交直线CD于点F.设DF=x,EC=y.
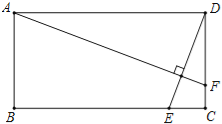
(1)求y关于x的函数关系式,并写出x的取值范围.
(2)当CF=1时,求EC的长.
(3)若直线AF与线段BC延长线交于点G,当△DBE与△DFG相似时,求DF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com