
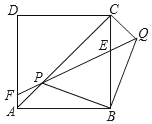
【题目】如图,正方形ABCD、等腰Rt△BPQ的顶点P在对角线AC上(点P与A、C不重合),QP与BC交于E,QP延长线与AD交于点F,连接CQ.
(1)①求证:AP=CQ;②求证:PA2=AFAD;
(2)若AP:PC=1:3,求tan∠CBQ.
【答案】(1)①证明见解析;②证明见解析;(2)![]()
【解析】整体分析:
(1)①用SAS证明△ABP≌△CBQ;②利用①的结论和△EPC与△EBQ组成的”8”字形证明△APF∽△ABP;(2)结合△ABP≌△CBQ,证∠PCQ=90°,由②可得∠CBQ=∠CPQ,又CQ=AP,根据正切的定义即可求解.
(1)①∵四边形ABCD是正方形,∴AB=CB,∠ABC=90°,∴∠ABP+∠PBC=90°,
∵△BPQ是等腰直角三角形,∴BP=BQ,∠PBQ=90°,∴∠PBC+∠CBQ=90°
∴∠ABP=∠CBQ,∴△ABP≌△CBQ,∴AP=CQ;
②∵四边形ABCD是正方形,∴∠DAC=∠BAC=∠ACB=45°,
∵∠PQB=45°,∠CEP=∠QEB,∴∠CBQ=∠CPQ,
由①得△ABP≌△CBQ,∠ABP=∠CBQ
∵∠CPQ=∠APF,∴∠APF=∠ABP,∴△APF∽△ABP,
![]()
(本题也可以连接PD,证△APF∽△ADP)
(2)由①得△ABP≌△CBQ,∴∠BCQ=∠BAC=45°,
∵∠ACB=45°,∴∠PCQ=45°+45°=90°
∴tan∠CPQ=![]() ,
,
由①得AP=CQ,
又AP:PC=1:3,∴tan∠CPQ![]() ,
,
由②得∠CBQ=∠CPQ,
∴tan∠CBQ=tan∠CPQ=![]() .
.


科目:初中数学 来源: 题型:
【题目】有一张长 9cm,宽 5cm 的长方形硬纸板,如图在长方形硬纸板的四个角上各截去一个边长为 0.5cm 的正方形,如图①所示,然后把它折叠成一个无盖的长方体小盒,如图②所示.

请问:
(1)折叠成一个无盖的长方体小盒的地面长.宽分别是多少?
(2)这个硬纸板折叠成的小盒容积是多大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,一次函数y1=x+2与反比例函数y2=![]() (x>0)的图象交于点A(a,5)
(x>0)的图象交于点A(a,5)
(1)确定反比例函数的表达式;
(2)结合图象,直接写出x为何值时,y1<y2
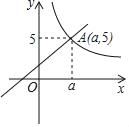
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的两个长方形用不同形式拼成图1和图2两个图形.
(1)若图1中的阴影部分面积为a2-b2;则图2中的阴影部分面积为 (用含字母a、b的代数式表示).

(2)由(1)你可以得到等式 .
(3)根据你所得到的等式解决下面的问题:
①计算:67.752-32.252;②解方程:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
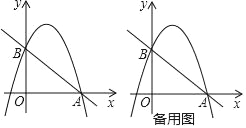
【题目】已知:如图,抛物线y=﹣x2+bx+C经过点B(0,3)和点A(3,0)
(1)求该抛物线的函数表达式和直线AB的函数表达式;
(2)若直线l⊥x轴,在第一象限内与抛物线交于点M,与直线AB交于点N,请在备用图上画出符合题意的图形,并求点M与点N之间的距离的最大值或最小值,以及此时点M,N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两个共一个顶点的等腰Rt△ABC,Rt△CEF,∠ABC=∠CEF=90°,连接AF,M是AF的中点,连接MB、ME.
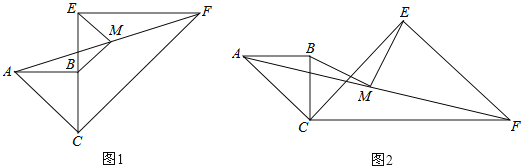
(1)如图1,当CB与CE在同一直线上时,求证:MB∥CF;
(2)如图1,若CB=a,CE=2a,求BM,ME的长;
(3)如图2,当∠BCE=45°时,求证:BM=ME.
查看答案和解析>>
科目:初中数学 来源: 题型:
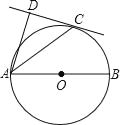
【题目】如图,AB为⊙O的直径,AB的长是4,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D.
(1)求证:AC平分∠DAB;
(2)若cos∠DAC=![]() ,求弧BC的长.
,求弧BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一条东西走向的商业街上,依次有书店(记为A)、冷饮店(记为B)、鞋店(记为C),冷饮店位于鞋店西边50m处,鞋店位于书店东边60m处,王平先去书店,然后沿着这条街向东走了30m至D处,接着向西走50m到达E处.
(1)以A为原点、向东为正方向画数轴,在数轴上表示出上述A,B,C,D,E的位置;
(2)若在这条街上建一家超市,使超市与鞋店C分居E点两侧,且到E点的距离相等,问超市在冷饮店的什么方向?距离多远?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com