
分析 (1)根据反比例函数的性质可知,当k>0时,函数图象在第一、三象限,当k<0时,函数图象在第二、四象限,从而可以解答本题;
(2)根据反比例函数的性质可知,当k<0时,y随x的增大而增大,从而可以解答本题.
解答 解:(1)∵在①y=$\frac{2}{x}$、②y=$\frac{1}{3x}$、④y=$\frac{3}{100x}$的k都>0,
∴在第一、三象限的是①②④,
∵③7y=-$\frac{10}{x}$中,k=$-\frac{10}{7}$<0,
∴在第二、四象限的是③,
故答案是:①②④,③;
(2)∵③7y=-$\frac{10}{x}$中,k=$-\frac{10}{7}$<0,
∴该函数的图象在第二、四象限,并且在每个象限内y随x的增大而增大,
故答案为③.
点评 本题考查反比例函数的性质,解题的关键是明确反比例函数的性质,会用性质解答问题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 两个分支关于原点成中心对称 | B. | 两个分支分布在第二、四象限 | ||
| C. | 两个分支关于x轴成轴对称 | D. | 必经过点(1,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,抛物线y=ax2-2x的对称轴为x=-1.
在平面直角坐标系xOy中,抛物线y=ax2-2x的对称轴为x=-1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在直角△ABC中,∠ACB=90°,点E在AC边上,连结BE,作∠ACF=∠CBE交AB于点F,同时点D在BE上,且CD⊥AB.
在直角△ABC中,∠ACB=90°,点E在AC边上,连结BE,作∠ACF=∠CBE交AB于点F,同时点D在BE上,且CD⊥AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
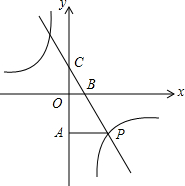 如图,一次函数y=kx+3的图象分别交x轴、y轴于点B、点C,与反比例函数y=$\frac{n}{x}$的图象在第四象限的相交于点P,并且PA⊥y轴于点A,已知A (0,-6),且S△CAP=18.
如图,一次函数y=kx+3的图象分别交x轴、y轴于点B、点C,与反比例函数y=$\frac{n}{x}$的图象在第四象限的相交于点P,并且PA⊥y轴于点A,已知A (0,-6),且S△CAP=18.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
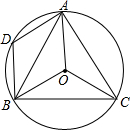 如图,在⊙0中,$\widehat{AB}$=$\widehat{AC}$,∠ACB=60°.
如图,在⊙0中,$\widehat{AB}$=$\widehat{AC}$,∠ACB=60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com