
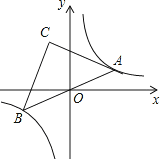
【题目】如图,点A是双曲线y=![]() 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为 .
在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为 .
【答案】y=﹣![]() .
.
【解析】
试题分析:连结OC,作CD⊥x轴于D,AE⊥x轴于E,设A点坐标为(a,![]() ),利用反比例函数的性质得到点A与点B关于原点对称,则OA=OB,再根据等腰直角三角形的性质得OC=OA,OC⊥OA,然后利用等角的余角相等可得到∠DCO=∠AOE,则根据“AAS”可判断△COD≌△OAE,所以OD=AE=
),利用反比例函数的性质得到点A与点B关于原点对称,则OA=OB,再根据等腰直角三角形的性质得OC=OA,OC⊥OA,然后利用等角的余角相等可得到∠DCO=∠AOE,则根据“AAS”可判断△COD≌△OAE,所以OD=AE=![]() ,CD=OE=a,于是C点坐标为(﹣
,CD=OE=a,于是C点坐标为(﹣![]() ,a),最后根据反比例函数图象上点的坐标特征确定C点所在的函数图象解析式.
,a),最后根据反比例函数图象上点的坐标特征确定C点所在的函数图象解析式.
试题解析:连结OC,作CD⊥x轴于D,AE⊥x轴于E,如图,
设A点坐标为(a,![]() ),
),
∵A点、B点是正比例函数图象与双曲线y=![]() 的交点,
的交点,
∴点A与点B关于原点对称,
∴OA=OB
∵△ABC为等腰直角三角形,
∴OC=OA,OC⊥OA,
∴∠DOC+∠AOE=90°,
∵∠DOC+∠DCO=90°,
∴∠DCO=∠AOE,
∵在△COD和△OAE中
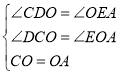
∴△COD≌△OAE(AAS),
∴OD=AE=![]() ,CD=OE=a,
,CD=OE=a,
∴C点坐标为(﹣![]() ,a),
,a),
∵﹣![]() a=﹣4,
a=﹣4,
∴点C在反比例函数y=﹣![]() 图象上.
图象上.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系XOY中,有A(3,2),B (﹣1,﹣4 ),P是X轴上的一点,Q是Y轴上的一点,若以点A,B,P,Q四个点为顶点的四边形是平行四边形,则Q点的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果店王阿姨到水果批发市场打算购进一种水果销售,经过还价,实际价格每千克比原来少2元,发现原来买这种80千克的钱,现在可买88千克。
(1)现在实际这种每千克多少元?
(2)准备这种,若这种的量y(千克)与单价x(元/千克)满足如图所示的一次函数关系。
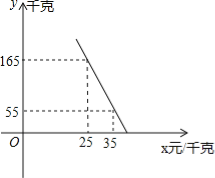
①求y与x之间的函数关系式;
②请你帮拿个主意,将这种的单价定为多少时,能获得最大利润?最大利润是多少?(利润=收入-进货金额)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将抛物线y=2(x﹣1)2+1先向左平移2个单位,再向上平移3个单位,则平移后抛物线的表达式是( )
A.y=2(x+1)2+4B.y=2(x﹣1)2+4
C.y=2(x+2)2+4D.y=2(x﹣3)2+4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列语句正确的是( )
A.两条直线相交,组成的图形叫做角
B.从同一点引出的两条射线组成的图形叫角
C.两条有公共点的射线组成的图形叫角
D.两条有公共端点的线段组成的图形叫角
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com