
 如图,⊙O为△ABC的外接圆,其中D点在$\widehat{AC}$上,且OD⊥AC,已知∠A=36°,∠C=60°,则∠BOD=156°.
如图,⊙O为△ABC的外接圆,其中D点在$\widehat{AC}$上,且OD⊥AC,已知∠A=36°,∠C=60°,则∠BOD=156°. 科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 50×10-7 | B. | 50×10-5 | C. | 50×10-3 | D. | 5×10-6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
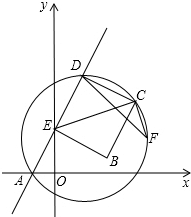 如图,直线y=2x+2与x轴,y轴分别交于A,E两点,D是第一象限内直线y=2x+2上运动的一个动点,以ED为边作正方形EDCB,连结CE,作EC⊥CF与过A,D,C三点的圆交于点F,连结DF.
如图,直线y=2x+2与x轴,y轴分别交于A,E两点,D是第一象限内直线y=2x+2上运动的一个动点,以ED为边作正方形EDCB,连结CE,作EC⊥CF与过A,D,C三点的圆交于点F,连结DF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 快、慢两车分别从相距480km的甲,乙两地同时出发,匀速行驶,相向而行,途中慢车因故停留了1小时,然后继续以原速驶向甲地,到达甲地后即停止行驶;快车到达乙地后,立即按原路原速返回甲地(调头时间忽略不计).如图是快、慢两车距乙地路程y(km)与所用时间x(h)之间的函数图象,则当两车第一次相遇时,快车距离甲地的路程是320千米.
快、慢两车分别从相距480km的甲,乙两地同时出发,匀速行驶,相向而行,途中慢车因故停留了1小时,然后继续以原速驶向甲地,到达甲地后即停止行驶;快车到达乙地后,立即按原路原速返回甲地(调头时间忽略不计).如图是快、慢两车距乙地路程y(km)与所用时间x(h)之间的函数图象,则当两车第一次相遇时,快车距离甲地的路程是320千米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
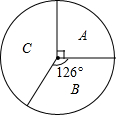 某校对1500名在校学生进行每周上网的情况调查,A为每天上网的学生,B为从不上网的学生,C为偶尔上网的学生,如扇形统计图所示.请根据图上信息,解答以下问题:
某校对1500名在校学生进行每周上网的情况调查,A为每天上网的学生,B为从不上网的学生,C为偶尔上网的学生,如扇形统计图所示.请根据图上信息,解答以下问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com