
【题目】已知二次函数y=ax2+bx﹣2的图象与x轴交于A,B两点,与y轴交于点C,点A的坐标为(4,0),且当x=﹣2和x=5时二次函数的函数值y相等.
(1)求实数a、b的值;
(2)如图1,动点E,F同时从A点出发,其中点E以每秒2个单位长度的速度沿AB边向终点B运动,点F以每秒 ![]() 个单位长度的速度沿射线AC方向运动.当点E停止运动时,点F随之停止运动.设运动时间为t秒.连接EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.
个单位长度的速度沿射线AC方向运动.当点E停止运动时,点F随之停止运动.设运动时间为t秒.连接EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.
①是否存在某一时刻t,使得△DCF为直角三角形?若存在,求出t的值;若不存在,请说明理由.
②设△DEF与△ABC重叠部分的面积为S,求S关于t的函数关系式.
【答案】
(1)解:由题意得 ![]()
解得: 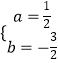 .
.
(2)解:①由(1)知二次函数为y= ![]() x2﹣
x2﹣ ![]() x﹣2
x﹣2
∵A(4,0),
∴B(﹣1,0),C(0,﹣2)
∴OA=4,OB=1,OC=2
∴AB=5,AC=2 ![]() ,BC=
,BC= ![]()
∴AC2+BC2=25=AB2
∴△ABC为直角三角形,且∠ACB=90°
∵AE=2t,AF= ![]() t,
t,
∴ ![]() =
= ![]() =
= ![]()
又∵∠EAF=∠CAB,
∴△AEF∽△ACB
∴∠AEF=∠ACB=90°
∴△AEF沿EF翻折后,点A落在x轴上点D处;
由翻折知,DE=AE,
∴AD=2AE=4t,EF= ![]() AE=t
AE=t
假设△DCF为直角三角形
当点F在线段AC上时
ⅰ)若C为直角顶点,则点D与点B重合,如图2
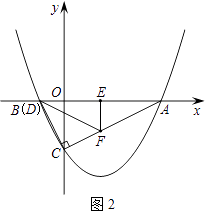
∴AE= ![]() AB=
AB= ![]() t=
t= ![]() ÷2=
÷2= ![]() ;
;
ⅱ)若D为直角顶点,如图3
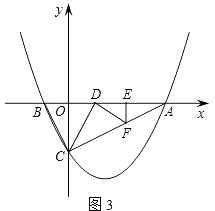
∵∠CDF=90°,
∴∠ODC+∠EDF=90°
∵∠EDF=∠EAF,
∴∠OBC+∠EAF=90°
∴∠ODC=∠OBC,
∴BC=DC
∵OC⊥BD,
∴OD=OB=1
∴AD=3,
∴AE= ![]()
∴t= ![]() ;
;
当点F在AC延长线上时,∠DFC>90°,△DCF为钝角三角形
综上所述,存在时刻t,使得△DCF为直角三角形,t= ![]() 或t=
或t= ![]() .
.
②ⅰ)当0<t≤ ![]() 时,重叠部分为△DEF,如图1、图2
时,重叠部分为△DEF,如图1、图2
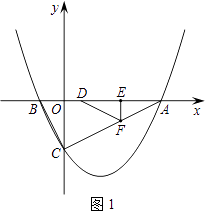
∴S= ![]() ×2t×t=t2;
×2t×t=t2;
ⅱ)当 ![]() <t≤2时,设DF与BC相交于点G,则重叠部分为四边形BEFG,如图4
<t≤2时,设DF与BC相交于点G,则重叠部分为四边形BEFG,如图4
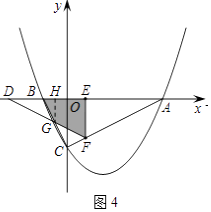
过点G作GH⊥BE于H,设GH=m
则BH= ![]() ,DH=2m,∴DB=
,DH=2m,∴DB= ![]()
∵DB=AD﹣AB=4t﹣5
∴ ![]() =4t﹣5,
=4t﹣5,
∴m= ![]() (4t﹣5)
(4t﹣5)
∴S=S△DEF﹣S△DBG= ![]() ×2t×t﹣
×2t×t﹣ ![]() (4t﹣5)×
(4t﹣5)× ![]() (4t﹣5)=﹣
(4t﹣5)=﹣ ![]() t2+
t2+ ![]() t﹣
t﹣ ![]() ;
;
ⅲ)当2<t≤ ![]() 时,重叠部分为△BEG,如图5
时,重叠部分为△BEG,如图5

∵BE=DE﹣DB=2t﹣(4t﹣5)=5﹣2t,GE=2BE=2(5﹣2t)
∴S= ![]() ×(5﹣2t)×2(5﹣2t)=4t2﹣20t+25.
×(5﹣2t)×2(5﹣2t)=4t2﹣20t+25.
【解析】(1)根据抛物线图象经过点A以及“当x=-2和x=5时二次函数的函数值y相等”两个条件,列出方程组求出待定系数的值即可解答.
(2)①首先由抛物线解析式能得到点A、B、C三点的坐标,则线段OA、OB、OC的长可求,进一步能得出AB、BC、AC的长;首先用t 表示出线段AD、AE、AF(即DF)的长,则根据AE、EF、OA、OC的长以及公共角∠OAC能判定△AEF、△AOC相似,那么△AEF也是一个直角三角形,及∠AEF是直角;若△DCF是直角,可分成三种情况讨论:
i)、点C为直角顶点,由于△ABC恰好是直角三角形,且以点C为直角顶点,所以此时点B、D重合,由此得到AD的长,进而求出t的值;
ii)、点D为直角顶点,此时∠CDB与∠CBD恰好是等角的余角,由此可证得OB=OD,再得到AD的长后可求出t的值;
iii)、点F为直角顶点,当点F在线段AC上时,∠DFC是锐角,而点F在射线AC的延长线上时,∠DFC又是钝角,所以这种情况不符合题意.
②此题需要分三种情况讨论:
i)、当点E在点A与线段AB中点之间时,两个三角形的重叠部分是整个△DEF;
ii)、当点E在线段AB中点与点O之间时,重叠部分是个不规则四边形,那么其面积可由大直角三角形与小钝角三角形的面积差求得;
iii)、当点E在线段OB上时,重叠部分是个小直角三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,AD是等腰△ABC底边BC上的高.点O是AC中点,延长DO到E,使OE=OD,连接AE,CE.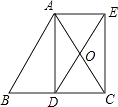
(1)求证:四边形ADCE的是矩形;
(2)若AB=17,BC=16,求四边形ADCE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后解答后面的问题.
我们知道方程2x+3y=12有无数组解,但在实际生活中我们往往只需要求出其正整数解.例:由2x+3y=12,得![]() ,(x、y为正整数)∴
,(x、y为正整数)∴![]() 则有0<x<6.又
则有0<x<6.又![]() 为正整数,则
为正整数,则![]() 为正整数.
为正整数.
由2与3互质,可知:x为3的倍数,从而x=3,代入![]() .
.
∴2x+3y=12的正整数解为![]()
问题:
(1)请你写出方程2x+y=5的一组正整数解:______;
(2)若![]() 为自然数,则满足条件的x值有______个;
为自然数,则满足条件的x值有______个;
A、2B、3C、4D、5
(3)七年级某班为了奖励学习进步的学生,购买了单价为3元的笔记本与单价为5元的钢笔两种奖品,共花费35元,问有几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去冬今春,某市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某乡中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件.
(1)求饮用水和蔬菜各有多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该乡中小学.已知每辆甲种货车最多可装饮用水40件和蔬菜10件,每辆乙种货车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两种商品原来的单价和为100元.因市场变化,甲商品降价10%,乙商品提价40%,调价后两种商品的单价和比原来的单价和提高了20%.甲、乙两种商品原来的单价各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司共有A,B,C三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图
各部门人数及每人所创年利润统计表
部门 | 员工人数 | 每人所创的年利润/万元 |
A | 5 | 10 |
B | b | 8 |
C | c | 5 |

(1)①在扇形图中,C部门所对应的圆心角的度数为
②在统计表中,b= , c=
(2)求这个公司平均每人所创年利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乘法公式的探究及应用:
数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片边长为![]() 的正方形,B种纸片是边长为
的正方形,B种纸片是边长为![]() 的正方形,C种纸片长为
的正方形,C种纸片长为![]() 宽为
宽为![]() 的长方形,并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形。
的长方形,并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形。
(1)请用两种不同的方法表示图2大正方形的面积:
方法1:_____________________;方法2:_____________________.
(2)观察图2,请你写出下列三个代数式:![]() 之间的等量关系;
之间的等量关系;
(3)类似的,请你用图1中的三种纸片拼一个图形验证:![]()
(4)根据(2)题中的等量关系,解决如下问题:
已知:![]() 求
求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD的一组对边AD、BC的延长线交于点E.
(1)如图1,若∠ABC=∠ADC=90°,求证:EDEA=ECEB;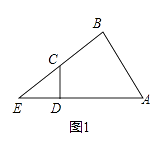
(2)如图2,若∠ABC=120°,cos∠ADC= ![]() ,CD=5,AB=12,△CDE的面积为6,求四边形ABCD的面积;
,CD=5,AB=12,△CDE的面积为6,求四边形ABCD的面积;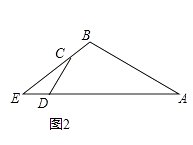
(3)如图3,另一组对边AB、DC的延长线相交于点F.若cos∠ABC=cos∠ADC= ![]() ,CD=5,CF=ED=n,直接写出AD的长(用含n的式子表示)
,CD=5,CF=ED=n,直接写出AD的长(用含n的式子表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com