
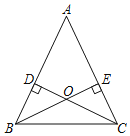
【题目】如图,锐角三角形ABC的两条高线BE、CD相交于点O,BE=CD.
(1)求证:BD=CE;
(2)判断点O是否在∠BAC的平分线上,并说明理由.
科目:初中数学 来源: 题型:
【题目】商场某种商品平均每天可销售30件,每件盈利50元。为了尽快减少库存,商场决定采取适当的降价措施。经调查发现,每件商品每降价1元,商场平均每天可多售出2件。设每件商品降价![]() 元。据此规律,请回答:
元。据此规律,请回答:
(1)商场日销售量增加_____件,每件商品盈利_____元(用含![]() 的代数式表示)。
的代数式表示)。
(2)在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到2100元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为宣传6月6日世界海洋日,某校八年级举行了主题为“珍海洋资源,保护海洋生物多科性“的知识党春活动,为了解此次宛赛成镇(百分制)的情况,随机抽取了部分参赛学生的成绩,整理并绘制出如下不完整的统计表和统计图(如图):

请根据图表信息解答以下问题:
(1)本次调查一共随机抽取了_____个参赛学生的成绩;
(2)a=_____,b=_____.
(3)所抽取的参赛学生的成绩的中位数落在的“组别”是_____
(4)请你估计,该校八年级全年级有500名学生,竞赛成绩达到80分以上(含80分)的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
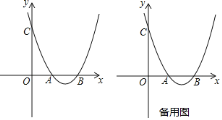
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
![]() 填空:
填空:![]() ________;
________;
![]() 点
点![]() 在抛物线上,且
在抛物线上,且![]() ,求
,求![]() 面积的最大值;
面积的最大值;
![]() 设
设![]() 为线段
为线段![]() 上一点(不含端点),连接
上一点(不含端点),连接![]() ,一动点
,一动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 以每秒一个单位速度运动到
以每秒一个单位速度运动到![]() 点,再沿线段
点,再沿线段![]() 以每秒
以每秒![]() 个单位的速度运动到
个单位的速度运动到![]() 后停止,当点
后停止,当点![]() 的坐标是多少时,点
的坐标是多少时,点![]() 在整个运动中用时最少?
在整个运动中用时最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
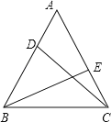
【题目】如图,在等边△ABC中,DE分别是边AB、AC上的点,且AD=CE,则∠ADC+∠BEA=( )
A.180°B.170°C.160°D.150°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为10,点E、F分别在边BC、CD上,且∠EAF=45°,AH⊥EF于点H,AH=10,连接BD,分别交AE、AH、AF于点P、G、Q.
(1)求△CEF的周长;
(2)若E是BC的中点,求证:CF=2DF;
(3)连接QE,求证:AQ=EQ.

查看答案和解析>>
科目:初中数学 来源: 题型:
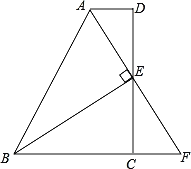
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;(2)AB=BC+AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等腰直角三角形ABC中,∠ACB=90°,BC=m,将边AB绕点B顺时针旋转90°得到线段BD,过点D作DE⊥CB交CB的延长线于点E,连接CD.
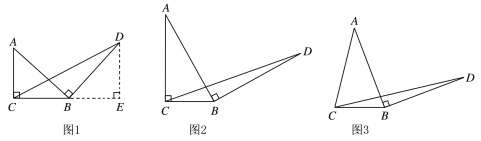
(1)直接写出△BCD的面积为 (用含m的式子表示).
(2)如图2,在一般的Rt△ABC中,∠ACB=90°,BC=m,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,用含m的式子表示△BCD的面积,并说明理由.
(3)如图3,在等腰△ABC中,AB=AC,BC=8,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,则△BCD的面积为 ;若BC=m,则△BCD的面积为 (用含m的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在网格中的位置如图所示(每个小正方形边长为1),AD⊥BC于D,下列选项中,错误的是( )

A. sinα=cosα B. tanC=2 C. sinβ=![]() D. tanα=1
D. tanα=1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com