
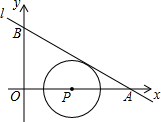
 我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:y=kx+3$\sqrt{3}$与轴、轴分别交于A、B,∠OAB=30°,点P在轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是4.
我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:y=kx+3$\sqrt{3}$与轴、轴分别交于A、B,∠OAB=30°,点P在轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是4. 分析 根据直线的解析式求得OB=3$\sqrt{3}$,进而求得OA=9,根据切线的性质求得PM⊥AB,根据∠OAB=30°,求得PM=$\frac{1}{2}$PA,然后根据“整圆”的定义,即可求得使得⊙P成为整圆的点P的坐标,从而求得点P个数.
解答 解:∵直线l:y=kx+3$\sqrt{3}$与x轴、y轴分别交于A、B,
∴B(0,3$\sqrt{3}$),
∴OB=3$\sqrt{3}$,
在Rt△AOB中,∠OAB=30°,
∴OA=$\sqrt{3}$OB=$\sqrt{3}$×3$\sqrt{3}$=9,
∵⊙P与l相切,设切点为M,连接PM,则PM⊥AB,
∴PM=$\frac{1}{2}$PA,
设P(x,0),
∴PA=9-x,
∴⊙P的半径PM=$\frac{1}{2}$PA=$\frac{9}{2}$-$\frac{1}{2}$x,
∵x为整数,PM为整数,
∴x可以取1,3,5,7,4个数,
∴使得⊙P成为整圆的点P个数是4.
故答案为4
点评 本题考查了切线的性质,含30°角的直角三角形的性质等,熟练掌握性质定理是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
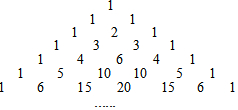 杨辉是我国南宋时期杰出的数学家和教育家,如图是杨辉在公元1261年著作《详解九章算法》里面的一张图,即“杨辉三角”,该图中有很多规律,请仔细观察,解答下列问题:
杨辉是我国南宋时期杰出的数学家和教育家,如图是杨辉在公元1261年著作《详解九章算法》里面的一张图,即“杨辉三角”,该图中有很多规律,请仔细观察,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 时间t(s) | 1 | 2 | 3 | 4 | |
| 距离s(m) | 2 | 8 | 18 | 32 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com