
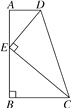
【题目】)如图,在四边形ABCD中,AD∥BC,∠ABC=90°,E是AB上一点,且DE⊥CE.
(1)求证:△ADE∽△BEC;
(2)若AD=1,DE=![]() ,BC=2,求AB的长.
,BC=2,求AB的长.
【答案】(1)证明见解析;
(2) AB=2![]() .
.
【解析】试题分析:
(1)由已知易证∠A=∠B=∠DEC=90°,由此可证∠AED=∠BCE,从而可证△ADE∽△BEC;
(2)在Rt△ADE中,由勾股定理可得:AE=![]() =
=![]() ,再由△ADE∽△BEC利用相似三角形的性质可求得BE,最后由AB=AE+BE可求得AB的长.
,再由△ADE∽△BEC利用相似三角形的性质可求得BE,最后由AB=AE+BE可求得AB的长.
试题解析:
(1)∵AD∥BC,∠ABC=90°,
∴∠A=90°.
∵DE⊥CE,
∴∠DEC=90°,
∴∠AED+∠BEC=90°.
∵∠AED+∠ADE=90°,
∴∠ADE=∠BEC,
∴△ADE∽△BEC.
(2)在Rt△ADE中,AE=![]() =
=![]() .
.
∵△ADE∽△BEC,
∴![]() ,即
,即![]() ,
,
∴BE=![]() ,
,
∴AB=AE+BE=2![]() .
.


 星级口算天天练系列答案
星级口算天天练系列答案科目:初中数学 来源: 题型:
【题目】(10分)如图,在直角坐标系xOy中,A(﹣1,0),B(3,0),将A,B同时分别向上平移2个单位,再向右平移1个单位,得到的对应点分别为D,C,连接AD,BC.

(1)直接写出点C,D的坐标:C ,D ;
(2)四边形ABCD的面积为 ;
(3)点P为线段BC上一动点(不含端点),连接PD,PO.求证:∠CDP+∠BOP=∠OPD.
查看答案和解析>>
科目:初中数学 来源: 题型:
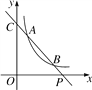
【题目】如图,已知直线y=ax+b与双曲线y=![]() (x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.
(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.
(1)若A,B两点的坐标分别为(1,3),(3,y2),求点P的坐标;
(2)若b=y1+1,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 和双曲线
和双曲线![]() (k为正整数)交于A,B两点.
(k为正整数)交于A,B两点.
(1)当k=1时,求A、B两点的坐标;
(2)当k=2时,求△AOB的面积;
(3)当k=1时,△OAB的面积记为S1,当k=2时,△OAB的面积记为S2,…,依此类推,当k=n时,△OAB的面积记为Sn,若S1+S2+…+Sn=![]() ,求n的值.
,求n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
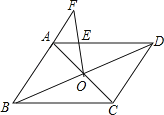
【题目】如图,在□ABCD中,对角线AC、BD相交于点O,过点O与AD上的一点E作直线OE,交BA的延长线于点F.若AD=4,DC=3,AF=2,则AE的长是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com