
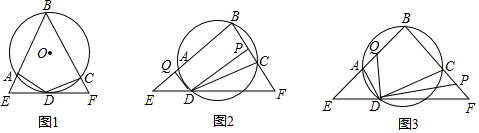
分析 (1)如图1中,连接BD.由BE=BF,ED=DF,推出∠DBE=∠DBF,推出$\widehat{AD}$=$\widehat{CD}$,推出AD=CD.
(2)如图2中,由△ADQ∽△CDP,推出$\frac{AQ}{PC}$=$\frac{QD}{DP}$,由tan∠F=$\sqrt{3}$,推出∠F=60°,由DF=2DE,设DE=a,则DF=2a,DQ=$\frac{1}{2}$a,DP=$\sqrt{3}$a,由此即可解决问题.
(3)如图3中,作DN⊥BC于N,DM⊥EB于M,连接BD.由△ADQ∽△CDP,推出$\frac{AQ}{PC}$=$\frac{DQ}{DP}$,∠AQD=∠DPC,由△DMQ∽△DNP,推出$\frac{DQ}{DP}$=$\frac{DM}{DN}$,推出$\frac{AQ}{PC}$=$\frac{DM}{DN}$,由$\frac{{S}_{△EDB}}{{S}_{△BDF}}$=$\frac{\frac{1}{2}•EB•DM}{\frac{1}{2}•BF•DN}$=$\frac{DE}{DF}$,由DE=m•DF,BE=k•BF,推出$\frac{k•BF•DM}{BF•DN}$=$\frac{m•DF}{DF}$,推出$\frac{DM}{DN}$=$\frac{m}{k}$,即可解决问题.
解答 (1)证明:如图1中,连接BD.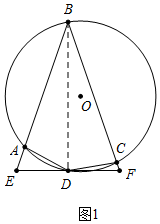
∵BE=BF,ED=DF,
∴∠DBE=∠DBF,
∴$\widehat{AD}$=$\widehat{CD}$,
∴AD=CD.
(2)如图2中,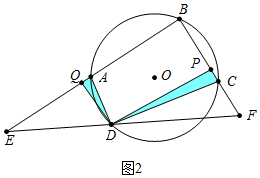
∵∠B=90°,∠B+∠ADC=180°,
∴∠QDP=∠ADC=90°,∵DPB=90°,
∴四边形ABPD是矩形,
∴∠AQD=∠DPC=90°,
∵∠ADC=∠QDP,
∴∠ADQ=∠CDP,
∴△ADQ∽△CDP,
∴$\frac{AQ}{PC}$=$\frac{QD}{DP}$,
∵tan∠F=$\sqrt{3}$,
∴∠F=60°,∵DF=2DE,
设DE=a,则DF=2a,DQ=$\frac{1}{2}$a,DP=$\sqrt{3}$a,
∴$\frac{AQ}{PC}$=$\frac{\frac{1}{2}a}{\sqrt{3}a}$=$\frac{\sqrt{3}}{6}$.
(3)如图3中,作DN⊥BC于N,DM⊥EB于M,连接BD.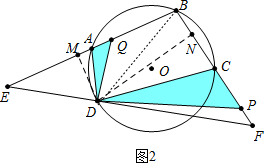
∵∠ADC=∠QDP,
∴∠ADQ=∠CDP,
∵∠DCP=∠DAQ,
∴△ADQ∽△CDP,
∴$\frac{AQ}{PC}$=$\frac{DQ}{DP}$,∠AQD=∠DPC,
∵∠DMQ=∠DNP,
∴△DMQ∽△DNP,
∴$\frac{DQ}{DP}$=$\frac{DM}{DN}$,
∴$\frac{AQ}{PC}$=$\frac{DM}{DN}$,
∵$\frac{{S}_{△EDB}}{{S}_{△BDF}}$=$\frac{\frac{1}{2}•EB•DM}{\frac{1}{2}•BF•DN}$=$\frac{DE}{DF}$,
∵DE=m•DF,BE=k•BF,
∴$\frac{k•BF•DM}{BF•DN}$=$\frac{m•DF}{DF}$,
∴$\frac{DM}{DN}$=$\frac{m}{k}$,
∴$\frac{AQ}{PC}$=$\frac{m}{k}$.
点评 本题考查圆综合题、等腰三角形的性质、相似三角形的判定和性质、特殊角的三角函数、矩形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造相似三角形解决问题,学会利用面积法证明线段之间的关系,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
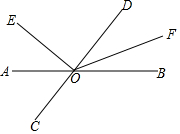 如图,直线AB,CD相交于点O,OE⊥CD,OF平分∠BOD.
如图,直线AB,CD相交于点O,OE⊥CD,OF平分∠BOD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
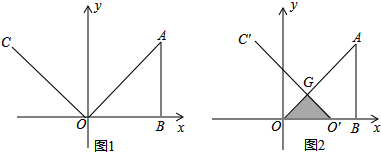
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
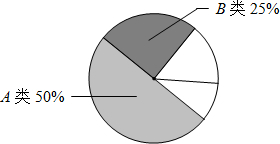 期末考试后,某市第一中学为了解本校九年级学生期末考试数学学科成绩情况,决定对该年级学生数学学科期末考试成绩进行抽样分析,已知九年级共有12个班,每班48名学生,请按要求回答下列问题:
期末考试后,某市第一中学为了解本校九年级学生期末考试数学学科成绩情况,决定对该年级学生数学学科期末考试成绩进行抽样分析,已知九年级共有12个班,每班48名学生,请按要求回答下列问题:| 成绩(单位:分) | 频数 | 频率 |
| A类(80~100) | $\frac{1}{2}$ | |
| B类(60~79) | $\frac{1}{4}$ | |
| C类(40~59) | 8 | $\frac{1}{6}$ |
| D类(0~39) | 4 | $\frac{1}{12}$ |
| 学校 | 平均数(分) | 极差(分) | 方差 | A、B类的频率和 |
| 第一中学 | 71 | 52 | 432 | 0.75 |
| 第二中学 | 71 | 80 | 497 | 0.82 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
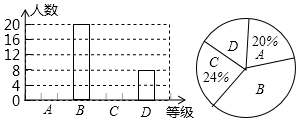 某校九年级一次模拟考试后,数学考试为了了解学生的学习情况,在全校1000名九年级学生中,随机抽取了50名学生的数学成绩进行统计分析,并绘制了如下统计表和统计图(部分信息未给全).
某校九年级一次模拟考试后,数学考试为了了解学生的学习情况,在全校1000名九年级学生中,随机抽取了50名学生的数学成绩进行统计分析,并绘制了如下统计表和统计图(部分信息未给全). | 成绩/分 | 111~120 | 101~110 | 91~100 | 90及90以下 |
| 等级 | A | B | C | D |
| 学生人数 | m | 20 | n | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
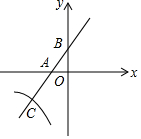 如图,已知一次函数${y}_{1}=\frac{4}{3}x+4$的图象分别交x轴于A、B两点,交反比例函数y2=$\frac{a}{x}$(x<0)的图象于第三象限的C点,且AB=AC.
如图,已知一次函数${y}_{1}=\frac{4}{3}x+4$的图象分别交x轴于A、B两点,交反比例函数y2=$\frac{a}{x}$(x<0)的图象于第三象限的C点,且AB=AC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com