
分析 (1)将分母中被开方数写成完全平方式,根据二次根式性质开方后分母有理化即可得;
(2)将x+1看做整体移项、合并后即可得x+1=0,从而得解.
解答 解:(1)原式=$\frac{1}{\sqrt{(\sqrt{2})^{2}+2×\sqrt{2}×\sqrt{3}+(\sqrt{3})^{2}}}$+$\frac{1}{\sqrt{{2}^{2}+2×2×\sqrt{3}+(\sqrt{3})^{2}}}$
=$\frac{1}{\sqrt{(\sqrt{2}+\sqrt{3})^{2}}}$+$\frac{1}{\sqrt{(2+\sqrt{3})^{2}}}$
=$\frac{1}{\sqrt{2}+\sqrt{3}}$+$\frac{1}{2+\sqrt{3}}$
=$\sqrt{3}$-$\sqrt{2}$+2-$\sqrt{3}$
=2-$\sqrt{2}$,
故答案为:2-$\sqrt{2}$;
(2)移项、合并,得:($\sqrt{2}-1$)(x+1)=0,
∴x+1=0,即x=-1,
故答案为:x=-1.
点评 本题主要考查二次根式的混合运算和解方程的能力,熟练掌握完全平方公式是解题的关键.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:初中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (-1,-1) | C. | (1,-1) | D. | (1,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在矩形ABCD中,AB=10,BC=8,E为AD边上的一点,沿CE将△CDE对折,使点D正好落在AB边上,记落点为F,求sin∠AFE的值.
如图,在矩形ABCD中,AB=10,BC=8,E为AD边上的一点,沿CE将△CDE对折,使点D正好落在AB边上,记落点为F,求sin∠AFE的值.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
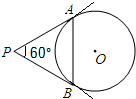 如图,从圆O外一点P引圆O的两条切线PA,PB,切点分别为A,B,如果∠APB=60°,PA=8,那么弦AB的长是( )
如图,从圆O外一点P引圆O的两条切线PA,PB,切点分别为A,B,如果∠APB=60°,PA=8,那么弦AB的长是( )| A. | 4 | B. | 4$\sqrt{3}$ | C. | 8 | D. | 8$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com