
【题目】四边形![]() 为矩形,连接
为矩形,连接![]() ,
,![]() ,点
,点![]() 在
在![]() 边上.
边上.
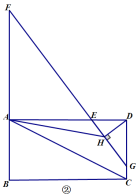
(1)如图①,若![]() ,
,![]() ,求
,求![]() 的面积;
的面积;
(2)如图②,延长![]() 至点
至点![]() ,使得
,使得![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,求证:
,求证:![]() ;
;
(3)如图③,将线段![]() 绕点
绕点![]() 旋转一定的角度
旋转一定的角度![]() (
(![]() )得到线段
)得到线段![]() ,连接
,连接![]() ,点
,点![]() 始终为
始终为![]() 的中点,连接
的中点,连接![]() .已知
.已知![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.


【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() .
.
【解析】
(1)根据30°的直角三角形求CD和ED,再利用面积公式求△AEC的面积;
(2)作辅助线,构建全等三角形,证明△AFM≌△ADH,得AM=AH,FM=DH,则△MAH是等腰直角三角形,有MH=![]() AH,根据线段的和代入得结论;
AH,根据线段的和代入得结论;
(3)分别计算DN的最大值和最小值,连接AC和BD交于O,当DN在BD上,可得DN的最大值和最小值.
解:(1)如图1,在Rt△EDC中,
∵∠ECD=30°,
∴![]() ,
,![]() ,
,
∴DC=ECcos30°=4×![]() =2
=2![]() ,
,
∴AE=2DC-ED=4![]() -2,
-2,
∴S△AEC=![]() ×AE×DC=
×AE×DC=![]() (4
(4![]() -2)×2
-2)×2![]() =12-2
=12-2![]() ;
;
(2)如图2,过A作AM⊥AH,交FG于M,
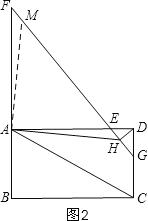
∴∠MAH=∠MAD+∠DAH=90°,
又∵∠FAD=∠MAD+∠FAM=90°,
∴∠FAM=∠DAH,
∵AF∥CD,
∴∠F=∠FGD
∵DH⊥EG,
∴∠DHE=∠HDG+∠FGD=90°,
∠EDG=∠EDH+∠HDG=90°,
∴∠FGD=∠EDH,
∴∠F=∠EDH,
又∵AF=2CD,AD=2CD,
∴AF=AD,
∴△AFM≌△ADH,
∴AM=AH,FM=DH,
∴△MAH是等腰直角三角形,
∴MH=![]() AH,
AH,
∵FH=MH+FM,
∴FH=![]() AH+DH;
AH+DH;
(3)∵线段AE绕点A旋转一定的角度α(0°<α<360°)得到线段AE′,
∴E'的运动轨迹是一个以点A为圆心半径为4的圆,
连接AC,BD交于点O,
∵点O、N为AC、CE′的中点,
∴ON=![]() AE′=2,
AE′=2,
∵CD=4,
∴BC=AD=2CD=8,
在Rt△BCD中,![]() ,
,
∴![]()
∴如图3,当DN在对角线BD上时,DN的长最小,DN=OD-ON=2![]() -2,
-2,
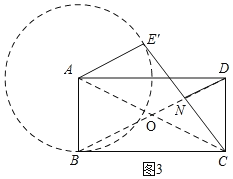
此时DN的值最小是2![]() -2;
-2;
当α>180°时,DN在BD上,如图4,DN最长,
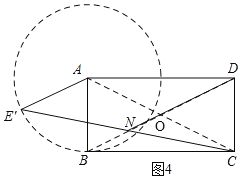
∴DN=OD+ON=2![]() +2,
+2,
∵0°<α<360°,
∴2![]() -2≤DN≤2
-2≤DN≤2![]() +2.
+2.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,已知点A(-1,0), B(0,![]() ),对△OAB连续作旋转变换,依次得到△1,△2,△3,△4,…,则△2019的直角顶点的坐标为______________.
),对△OAB连续作旋转变换,依次得到△1,△2,△3,△4,…,则△2019的直角顶点的坐标为______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,函数![]() (x>0)的图象与直线l1:
(x>0)的图象与直线l1:![]() 交于点A,与直线l2:x=k交于点B.直线l1与l2交于点C.
交于点A,与直线l2:x=k交于点B.直线l1与l2交于点C.

(1) 当点A的横坐标为1时,则此时k的值为 _______;
(2) 横、纵坐标都是整数的点叫做整点. 记函数![]() (x>0) 的图像在点A、B之间的部分与线段AC,BC围成的区域(不含边界)为W.
(x>0) 的图像在点A、B之间的部分与线段AC,BC围成的区域(不含边界)为W.
①当k=3时,结合函数图像,则区域W内的整点个数是_________;
②若区域W内恰有1个整点,结合函数图象,直接写出k的取值范围:___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校数学兴趣小组的同学要测量建筑物![]() 的高度,如图,建筑物
的高度,如图,建筑物![]() 前有一段坡度为
前有一段坡度为![]() 的斜坡
的斜坡![]() ,小明同学站在斜坡上的
,小明同学站在斜坡上的![]() 点处,用测角仪测得建筑物屋顶
点处,用测角仪测得建筑物屋顶![]() 的仰角为
的仰角为![]() ,接着小明又向下走了
,接着小明又向下走了![]() 米,刚好到达坡底
米,刚好到达坡底![]() 处,这时测到建筑物屋顶
处,这时测到建筑物屋顶![]() 的仰角为
的仰角为![]() ,
,![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 在同一平面内.若测角仪的高度
在同一平面内.若测角仪的高度![]() 米,则建筑物
米,则建筑物![]() 的高度约为( ).(精确到0.1米,参考数据:
的高度约为( ).(精确到0.1米,参考数据:![]() ,
,![]() ,
,![]() )
)
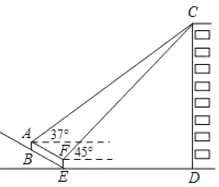
A.38.6B.39.0C.40.0D.41.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《中国诗词大会》以“赏中华诗词、寻文化基因、品生活之美”为基本宗旨,力求通过对诗词知识的比拼及赏析,带动全民重温那些曾经学过的古诗词,分享诗词之美,感受诗词之趣,从古人的智慧和情怀中汲取营养,涵养心灵,自开播以来深受广大师生的喜爱.某学校为了提高学生的诗词水平,倡导全校3000名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛.为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根据调查结果绘制成的条形和扇形统计图如图所示.
(整理、描述数据):

大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”:
一周诗词背数量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人数 | 16 | 24 | 32 | 78 |
| 35 |
(分析数据):
平均数 | 中位数 | 众数 | |
大赛之前 | 5 |
|
|
大赛之后 | 6 | 6 | 6 |
请根据调查的信息
(1)补全条形统计图;
(2)计算![]() 首,
首,![]() 首,
首,![]() 首,并估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;
首,并估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;
(3)根据调査的相关数据,选择适当的统计量评价该校经典诗词诵背系列活动的效果.
查看答案和解析>>
科目:初中数学 来源: 题型:
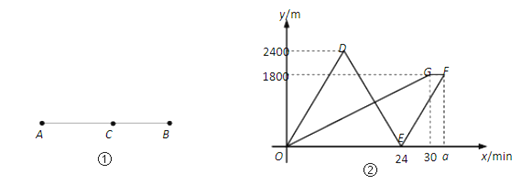
【题目】如图①,点A表示小明家,点B表示学校.小明妈妈骑车带着小明去学校,到达C处时发现数学书没带,于是妈妈立即骑车原路回家拿书后再追赶小明,同时小明步行去学校,到达学校后等待妈妈.假设拿书时间忽略不计,小明和妈妈在整个运动过程中分别保持匀速.妈妈从C处出发x分钟时离C处的距离为y1米,小明离C处的距离为y2米,如图②,折线O-D-E-F表示y1与x的函数图像;折线O-G-F表示y2与x的函数图像.
(1)小明的速度为 m/min,图②中a的值为 .
(2)设妈妈从C处出发x分钟时妈妈与小明之间的距离为y米.当12≤x≤30时,求出y与x的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店老板准备购买A、B两种型号的足球共100只,已知A型号足球进价每只40元,B型号足球进价每只60元.
(1)若该店老板共花费了5200元,那么A、B型号足球各进了多少只;
(2)若B型号足球数量不少于A型号足球数量的![]() ,那么进多少只A型号足球,可以让该老板所用的进货款最少?
,那么进多少只A型号足球,可以让该老板所用的进货款最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系xOy中,抛物线![]() 经过点A(5,0)、B(-3,4),抛物线的对称轴与x轴相交于点D.
经过点A(5,0)、B(-3,4),抛物线的对称轴与x轴相交于点D.
(1)求抛物线的表达式;
(2)联结OB、BD.求∠BDO的余切值;
(3)如果点P在线段BO的延长线上,且∠PAO =∠BAO,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com