
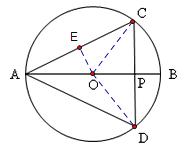
【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足为P,若AB=2,AC=![]() .
.
(1)求∠A的度数.
(2)求弧CBD的长.
(3)求弓形CBD的面积.

【答案】(1)∠A=30°;(2)![]() ;(3)
;(3)![]() -
-![]() .
.
【解析】试题分析:(1)过O作OE⊥AC,由垂径定理可得AE的长,再用三角函数即可求得∠A的度数;
(2)由∠A得度数得出对应圆心角∠COB的度数,由垂径定理得∠DOB=∠COB,由此得到∠COD的度数,用弧长公式即可求出弧长;
(3)由公式:弓形CBD的面积=扇形COD的面积△COD的面积,即可求出弓形面积.
试题解析:(1)过O作OE⊥AC,
![]() ,
,
![]()
在Rt△AEO中, ![]()
![]()
(2)连结OC,OD, ![]()
![]()
∵AB是⊙O的直径,弦CD⊥AB,
∴![]() =
=![]() ,
,
![]()
![]()
∵AB=2,
![]()
∴![]() 的长=
的长=![]() ;
;
(3) ![]() OP⊥CD,
OP⊥CD,
![]()
∵OC=1,
![]()
![]() ,
,
∴弓形CBD的面积=扇形COD的面积△COD的面积![]()


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点分别为A(2,3)、B(4,2)、C(﹣2,﹣3)
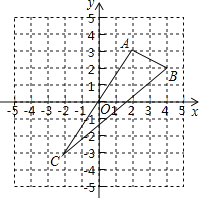
(1)写出A点关于x轴对称的点的坐标 ;写出B点关于y轴对称的点的坐标 .
(2)请在图中作出△ABC关于x轴对称的△DEF(A、B、C的对应点分别是D、E、F);
(3)求三角形ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学课上,张老师出示了一个题目:“如图,ABCD的对角线相交于点O,过点O作EF垂直于BD交AB,CD分别于点F,E,连接DF,BE.请根据上述条件,写出一个正确结论.”其中四位同学写出的结论如下:
小青:OE=OF;小何:四边形DFBE是正方形;
小夏:S四边形AFED=S四边形FBCE;小雨:∠ACE=∠CAF.
这四位同学写出的结论中不正确的是( )

A. 小青 B. 小何 C. 小夏 D. 小雨
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AC上取点B,在其同一侧作两个等边三角形△ABD 和△BCE ,连接AE,CD与GF,下列结论正确的有( )

① AE DC;②AHC120;③△AGB≌△DFB;④BH平分AHC;⑤GF∥AC
A.①②④B.①③⑤C.①③④⑤D.①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,轮船从A港出发,以28海里/小时的速度向正北方向航行,此时测的灯塔M在北偏东30°的方向上.半小时后,轮船到达B处,此时测得灯塔M在北偏东60°的方向上.
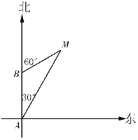
(1)求轮船在B处时与灯塔M的距离;
(2)轮船从B处继续沿正北方向航行,又经半小时后到达C处.求:此时轮船与灯塔M的距离是多少?灯塔M在轮船的什么方向上?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区改善生态环境,实行生活垃圾的分类处理,将生活垃圾分成三类:厨房垃圾、可回收垃圾和其他垃圾,分别记为m,n,p,并且设置了相应的垃圾箱,“厨房垃圾”箱,“可回收垃圾”箱和“其他垃圾”箱,分别记为A,B,C.
(1)若将三类垃圾随机投入三类垃圾箱,请用画树状图的方法求垃圾投放正确的概率;
(2)为了了解居民生活垃圾分类投放的情况,现随机抽取了小区三类垃圾箱中总共1 000吨生活垃圾,数据统计如下(单位:吨):
A | B | C | |
m | 400 | 100 | 100 |
n | 30 | 240 | 30 |
p | 20 | 20 | 60 |
请根据以上信息,试估计“厨房垃圾”投放正确的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.

(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为________;
(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠C=90°, BC=10,AC=6,过点A作BC的平行线l,P为直线l上的动点,且△BCP是等腰三角形,则AP的长为_____

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com