
【题目】已知:点E是正方形ABCD中边AB的中点.
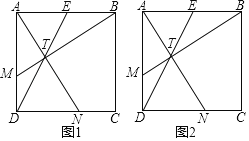
(1)如图1,点T为线段DE上一点,连接BT并延长交AD于点M,连接AT并延长交CD于点N,且AM=DN.试判断线段AN与线段BM的关系,并证明;求证:点M是线段AD的黄金分割点.
(2)如图2,在AD边上取一点M,满足AM2=DMDA时,连接BM交DE于点T,连接AT并延长交DC于点N,求tan∠MTD的值.
【答案】(1)AN=BM,AN⊥BM;证明见解析;(2)![]()
【解析】
(1)AN=BM,AN⊥BM.根据题目给出的条件证明△ABM≌△DAN,从而得出AN=BM,∠ABM=∠DAN,进而得出∠BAN+∠DAN=90°,得出∠ATB=90°,从而得出AN⊥BM;根据题目给出的条件证明△MDT~△TDA,得出DT2=MDAD,再证明DT=AM,即可证明点M是线段AD的黄金分割点;
(2)延长BM,CD交于点F,证明△FMD~△BMA,得出DMAB=AMDF,再根据AB∥CD得出DF=DN=AM,进而证明△ABM≌△DAN,可得∠ATB=90°,证得∠ABM=∠ETB=∠MTD,不妨设正方形的边长为1.设AM=x,由AM2=MDAD,得x2=(1-x)1,求出AM的值,然后根据锐角三角函数的定义解答即可.
解:(1)AN=BM,AN⊥BM.
理由如下:
∵四边形ABCD是正方形,
∴AB=DA,∠BAD=∠ADC=90°,又AM=DN,
∴△ABM≌△DAN(SAS),
∴∠ABM=∠DAN,AN=BM
又∠BAD=90°即∠BAN+∠DAN=90°,
∴∠BAN+∠ABM=90°
∴∠ATB=90°,
∴AN⊥BM
∴AN=BM,AN⊥BM;
证明:∵∠ATB=90°,M是AB中点.
∴TE=BE=AE,
∴∠EBT=∠ETB,∠EAT=∠ATE,
又∠ABM=∠DAN,∠ETB=∠MTD,
∴∠MTD=∠DAN,
又∠MDT=∠ADT,
∴△MDT~△TDA,
∴![]() ,
,
∴DT2=MDAD,
由AB∥CD,可得∠TND=∠EAT,又∠EAT=∠ATE,∠ATE=∠DTN,
∴∠TND=∠DTN
∴DT=DN,又AM=DN,
∴DT=AM,
又DT2=MDAD,
∴AM2=MDAD,
∴![]() ,
,
∴点M是线段AD的黄金分割点;
(2)延长BM,CD交于点F,如图.

∵四边形ABCD是正方形,AB∥CD,
∴∠F=∠MBA,又∠FMD=∠AMB,
∴△FMD~△BMA,
∴![]() ,即DMAB=AMDF,
,即DMAB=AMDF,
∵AB=AD,AM2=DMAD,
∴AM=DF,
由AB∥CF知![]() ,
,
又AE=BE,
∴DF=DN=AM,
由AB=AD,∠BAM=∠ADN=90°,DN=AM,可证△ABM≌△DAN(SAS),
∴∠ABM=∠DAN,
∴∠ABT+∠TAB=∠TAB+∠DAN=∠span>BAD=90°,
∴∠ATB=90°,
又AE=BE,
∴BE=ET,
∴∠ABM=∠ETB=∠MTD,
设正方形的边长为1.设AM=x,由AM2=MDAD,
得x2=(1﹣x)1,
![]() ,
,
又负值不合题意,舍去.
∴![]() ,
,
∴![]() ,
,
在Rt△ABM中,![]()
又∠ABM=∠MTD,
∴![]() .
.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在正方形ABCD中,G为CD边中点,连接AG并延长交BC边的延长线于E点,对角线BD交AG于F点.已知FG=2,则线段AE的长度为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
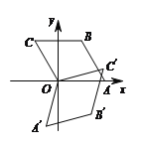
【题目】如图,菱形OABC的顶点O在坐标原点,顶点A在x轴上,∠B=120°,OA=4,将菱形OABC绕原点顺时针旋转105°至OA′B′C′的位置,则点B′的坐标为( )
A. (2![]() ,﹣2
,﹣2![]() )B. (
)B. (![]() ,-
,-![]() )C. (2,﹣2)D. (
)C. (2,﹣2)D. (![]() ,-
,-![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+6与y轴交于点A,与x轴交于点B,点E为线段AB的中点,∠ABO的平分线BD与y轴相交于点D,A、C两点关于x轴对称.
x+6与y轴交于点A,与x轴交于点B,点E为线段AB的中点,∠ABO的平分线BD与y轴相交于点D,A、C两点关于x轴对称.

(1)一动点P从点E出发,沿适当的路径运动到直线BC上的点F,再沿适当的路径运动到点D处.当P的运动路径最短时,求此时点F的坐标及点P所走最短路径的长;
(2)点E沿直线y=3水平向右运动得点E',平面内是否存在点M使得以D、B、M、E'为顶点的四边形为菱形,若存在,请直接写出点E′的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB是⊙O的直径,点C是弧AB的中点,点D是弧BC的中点,连接AC,BC,AD,BD,且AD与BC相交于点F,延长AC至E,使AC=EC,连接EB交AD的延长线于点G.
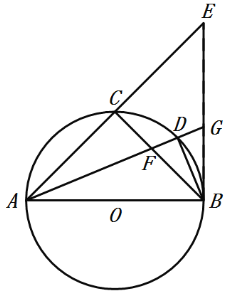
(1)求证:EB是⊙O的切线;
(2)求证;AF=2BD;
(3)求证:线段BG是线段CF和线段EG的比例中项.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数的图象与反比例函数的图象交于A(﹣2,1),B(1,n)两点.
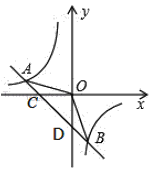
根据以往所学的函数知识以及本题的条件,你能提出求解什么问题?并解决这些问题(至少三个问题).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB∥CD,∠B=90°,AB=1,CD=2,BC=m,点P是边BC上一动点,若△PAB与△PCD相似,且满足条件的点P恰有2个,则m的值为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(Ⅰ)已知![]() ,若二次函数图象与
,若二次函数图象与![]() 轴有唯一公共点,求
轴有唯一公共点,求![]() 的值;
的值;
(Ⅱ)已知![]() .
.
(ⅰ)当![]() 时,二次函数图象与
时,二次函数图象与![]() 轴有且只有一个公共点,求
轴有且只有一个公共点,求![]() 的取值范围;
的取值范围;
(ⅱ)当![]() 时,
时,![]() 有最小值
有最小值![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com