
分析 (1)设原计划有x人参加植树活动,则实际参加人数为1.5人,根据原计划每人植树棵数-实际每人植树棵数=2,列方程求解即可;
(2)设原计划每人栽y棵树,则实际每人栽(y-2)棵树,根据实际参加植树活动的人数比原计划增加了50%列出方程即可.
解答 解:设原计划有x人参加植树活动,则实际参加人数为1.5x人.
根据题意得:$\frac{180}{x}$-$\frac{180}{1.5x}$=2,
解得 x=30.
经检验:x=30是方程的解,
所以x=30.
则1.5x=45.
答:实际有45人参加了这次植树活动;
(2)设原计划每人栽y棵树,则实际每人栽(y-2)棵树,根据题意得
1.5×$\frac{180}{y}$=$\frac{180}{y-2}$.
故答案为1.5×$\frac{180}{y}$=$\frac{180}{y-2}$.
点评 此题考查了分式方程的应用,关键在寻找相等关系,列出方程,在解方程时要注意检验.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
| 年数n | 高度h(厘米) |
| 第1年 | 100 |
| 第2年 | 100+5 |
| 第3年 | 100+10 |
| 第4年 | 100+15 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
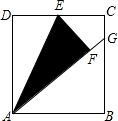 如图,在矩形ABCD中,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部.将AF延长交边BC于点G.若$\frac{CG}{BG}$=$\frac{1}{4}$,则$\frac{AD}{AB}$=( )
如图,在矩形ABCD中,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部.将AF延长交边BC于点G.若$\frac{CG}{BG}$=$\frac{1}{4}$,则$\frac{AD}{AB}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{6}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 4月份商场的商品销售总额是75万元 | |
| B. | 1月份商场服装部的销售额是22万元 | |
| C. | 5月份商场服装部的销售额比4月份减少了 | |
| D. | 3月份商场服装部的销售额比2月份减少了 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
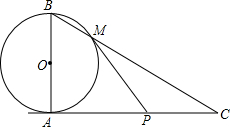 已知⊙O的直径AB=6,直线AC与⊙O相切于点A,线段AC=8,CB与⊙O相交于点M,⊙O的切线MP与AC相交于点P.
已知⊙O的直径AB=6,直线AC与⊙O相切于点A,线段AC=8,CB与⊙O相交于点M,⊙O的切线MP与AC相交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置,点A1、A2、A3和点C1、C2、C3、…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则B4的坐标是(15,8),B2015的坐标是(22015-1,22014).
正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置,点A1、A2、A3和点C1、C2、C3、…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则B4的坐标是(15,8),B2015的坐标是(22015-1,22014).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com