
【题目】如图,AD是⊙O的弦,AC是⊙O直径,⊙O的切线BD交AC的延长线于点B,切点为D,∠DAC=30°.
(1)求证:△ADB是等腰三角形;
(2)若BC= ![]() ,则AD的长为 .
,则AD的长为 .
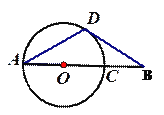
【答案】(1)见解析;(2)3
【解析】
试题(1)连接OD,由OA=OD,∠DAC=30°, 从而可得 ∠DOC =60°,再由BD是⊙O的切线,可得∠ODB=90°,从而可得∠B=30°,问题得证;
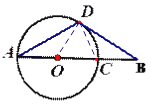
(2)连接CD,由AC是直径得∠ADC=90°,从而可得∠ACD=60°,再根据三角形的外角以及∠B=30°从而可得CD=CB=![]() ,再利用勾股定理即可得解.
,再利用勾股定理即可得解.
试题解析:(1)连接OD,∵∠DAC=30°, ∴∠ADO=∠DAC =30°, ∠DOC =60°,
∵BD是⊙O的切线,∴OD⊥BD,即∠ODB=90°,∴∠B=30°,
∴∠DAC=∠B ∴DA=DB, 即△ADB是等腰三角形;
(2)连接CD,∵AC是直径,∴∠ADC=90°,∵∠A=30°,∴∠ACD=60°,∵∠ACD=∠B+∠BDC,∵∠B=30°,∴∠BDC=30°=∠B,∴CD=CB=![]() ,∴AC=2CD=2
,∴AC=2CD=2![]() ,
,
∴AD=![]() =3.
=3.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】口袋中有![]() 只乒乓球,其中
只乒乓球,其中![]() 只是红球,另
只是红球,另![]() 只是黄球,它们的大小都一样,现从中任意摸出
只是黄球,它们的大小都一样,现从中任意摸出![]() 只球,
只球,
(1)恰为一红一黄的概率是多少?
(2)两只均为红球的概率是多少?
(3)两只均为黄球的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
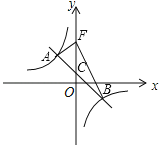
【题目】在平面直角坐标系中,一次函数y=﹣x+b的图象与反比例函数y=![]() (k≠0)的图象交于A、B点,与y轴交于点C,其中点A的半标为(﹣2,3)
(k≠0)的图象交于A、B点,与y轴交于点C,其中点A的半标为(﹣2,3)
(1)求一次函数和反比例函数的解析式;
(2)如图,若将点C沿y轴向上平移4个单位长度至点F,连接AF、BF,求△ABF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,等边△ABC中D点为AB边上一动点,E为直线AC上一点,将△ADE沿着DE折叠,点A落在直线BC上,对应点为F,若AB=4,BF:FC=1:3,则线段AE的长度为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
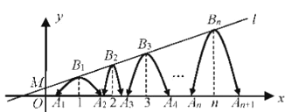
【题目】定义:若抛物线的顶点与![]() 轴的两个交点构成的三角形是直角三角形,则这种抛物线就称为“美丽抛物线”.如图,直线
轴的两个交点构成的三角形是直角三角形,则这种抛物线就称为“美丽抛物线”.如图,直线![]() :
:![]() 经过点
经过点![]() 一组抛物线的顶点
一组抛物线的顶点![]() ,
,![]() ,
,![]() ,…
,…![]() (
(![]() 为正整数),依次是直线
为正整数),依次是直线![]() 上的点,这组抛物线与
上的点,这组抛物线与![]() 轴正半轴的交点依次是:
轴正半轴的交点依次是:![]() ,
,![]() ,
,![]() ,…
,…![]() (
(![]() 为正整数).若
为正整数).若![]() ,当
,当![]() 为( )时,这组抛物线中存在美丽抛物线.
为( )时,这组抛物线中存在美丽抛物线.
A.![]() 或
或![]() B.
B.![]() 或
或![]() C.
C.![]() 或
或![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() .
.
![]() 抛物线的开口向____ 、对称轴为直线_ _、顶点坐标__ _;
抛物线的开口向____ 、对称轴为直线_ _、顶点坐标__ _;
![]() 当
当![]() ___ _时,函数有最___ 值,是__ _;
___ _时,函数有最___ 值,是__ _;
![]() 当
当![]() _ _ ______时,
_ _ ______时,![]() 随
随![]() 的增大而增大;当
的增大而增大;当![]() ____ __时,
____ __时,![]() 随
随![]() 的增大而减小;
的增大而减小;
![]() 该函数图象可由
该函数图象可由![]() 的图象经过怎样的平移得到的?
的图象经过怎样的平移得到的?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com