
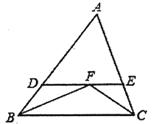
【题目】如图,![]() 中,
中,![]() 与
与![]() 的平分线交于点
的平分线交于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,那么下列结论:
,那么下列结论:
①![]() 是等腰三角形;②
是等腰三角形;②![]() ;
;
③若![]() ,
,![]() ;④
;④![]() .
.
其中正确的有( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
【答案】B
【解析】
根据角平分线的定义和平行线的性质可得∠DBF =∠DFB,∠ECF=∠EFC,然后利用等角对等边即可得出DB=DF,EF=EC,从而判断①和②;利用三角形的内角和定理即可求出∠ABC+∠ACB,然后利用角平分线的定义和三角形的内角和定理即可求出∠BFC,从而判断③;然后根据∠ABC不一定等于∠ACB即可判断④.
解:∵![]() 与
与![]() 的平分线交于点
的平分线交于点![]() ,
,
∴∠DBF=∠FBC,∠ECF=∠FCB
∵![]()
∴∠DFB=∠FBC,∠EFC=∠FCB
∴∠DBF =∠DFB,∠ECF=∠EFC
∴DB=DF,EF=EC,
即![]() 是等腰三角形,故①正确;
是等腰三角形,故①正确;
∴DE=DF+EF= BD+CE,故②正确;
∵∠A=50°
∴∠ABC+∠ACB=180°-∠A=130°
∴∠FBC+∠FCB=![]() (∠ABC+∠ACB)=65°
(∠ABC+∠ACB)=65°
∴∠BFC=180°-(∠FBC+∠FCB)=115°,故③正确;
∵∠ABC不一定等于∠ACB
∴∠FBC不一定等于∠FCB
∴BF不一定等于CF,故④错误.
正确的有①②③,共3个
故选B.


科目:初中数学 来源: 题型:
【题目】在如图的正方形网格中,每一个小正方形的边长均为 1.格点三角形 ABC(顶点是网格线交点的三角形)的顶点 A、C 的坐标分别是(﹣2,0),(﹣3,3).
(1)请在图中的网格平面内建立平面直角坐标系,写出点 B 的坐标;
(2)把△ABC 绕坐标原点 O 顺时针旋转 90°得到△A1B1C1,画出△A1B1C1,写出点
B1的坐标;
(3)以坐标原点 O 为位似中心,相似比为 2,把△A1B1C1 放大为原来的 2 倍,得到△A2B2C2 画出△A2B2C2,使它与△AB1C1 在位似中心的同侧;
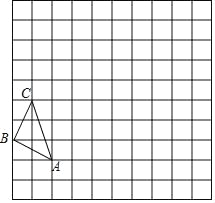
请在 x 轴上求作一点 P,使△PBB1 的周长最小,并写出点 P 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区准备五一组织社区内老年人去到县参加采摘节,现有甲、乙两家旅行社表示对老年人优惠,甲旅行社的优惠方式为:在原来每人100元的基础上,每人按照原价的60%收取费用;乙旅行社的优惠方式为:在收取一个600元固定团费的基础上,再额外收取每人40元.设参加采摘节的老年人有x人,甲、乙两家旅行社实际收费为![]() 元、
元、![]() 元.
元.
(Ⅰ)根据题意,填写下表:
老年人数量(人) | 5 | 10 | 20 | |
甲旅行社收费(元) | 300 | |||
乙旅行社收费)(元) | 800 |
(Ⅱ)求![]() 、
、![]() 关于x的函数关系式(不用写出自变量的取值范围)?
关于x的函数关系式(不用写出自变量的取值范围)?
(Ⅲ)如果![]() ,选择哪家旅行社合算?
,选择哪家旅行社合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
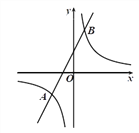
【题目】如图,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 与反比例函数
与反比例函数![]() 交于点
交于点![]() ,
, ![]() .
.
(1)分别求出反比例函数和一次函数的表达式;
(2)根据函数图象,直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县为落实“精准扶贫惠民政策”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合作施工15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙两队合作完成.则甲、乙两队合作完成该工程需要多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线![]() 、
、![]() 交于点
交于点![]() ,顺次联结ABCD各边中点得到的一个新的四边形,如果添加下列四个条件中的一个条件:①
,顺次联结ABCD各边中点得到的一个新的四边形,如果添加下列四个条件中的一个条件:①![]() ⊥
⊥![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,可以使这个新的四边形成为矩形,那么这样的条件个数是()
,可以使这个新的四边形成为矩形,那么这样的条件个数是()

A. 1个;B. 2个;
C. 3个;D. 4个.
查看答案和解析>>
科目:初中数学 来源: 题型:
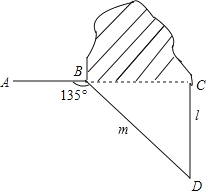
【题目】如图,修公路遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过C点作直线AB的垂线L,过点B作一直线(在山的旁边经过),与L相交于D点,经测量∠ABD=135°,BD=800米,求直线L上距离D点多远的C处开挖?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△![]() 中,作
中,作![]() ,边CD、BD交于点D,连接AD.
,边CD、BD交于点D,连接AD.
(1)请直接写出![]() 的度数;
的度数;
(2)求![]() 的度数;
的度数;
(3)用等式表示线段AC、BD、CD三者之间的数量关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com