
【题目】如图,已知A(-4,2)、B(n,-4)是一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象的两个交点.
的图象的两个交点.
(1)求此反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围.
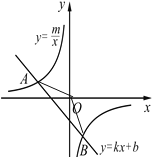
【答案】(1)、y=-![]() ;y=-x-2;(2)、6;(3)、x<-4或0<x<2
;y=-x-2;(2)、6;(3)、x<-4或0<x<2
【解析】
试题分析:(1)、根据点B的坐标得出反比例函数解析式;根据点A和点B的坐标利用待定系数法求出一次函数的解析式;(2)、利用△AOC的面积加上△BOC的面积得出答案;(3)、根据图像得出答案.
试题解析:(1)、B(2,-4)在反比例函数y=![]() 的图像上 所以-4=
的图像上 所以-4=![]() 得m=-8
得m=-8
所以反比例函数的解析式为:y=-![]() 当x=-4时, y=2,所以A(-4,2)
当x=-4时, y=2,所以A(-4,2)
因A、B两点都在一次函数y=kx+b的图象上 所以:![]() ,解得: k=-1,b=-2
,解得: k=-1,b=-2
所以这个一次函数的解析式为: y=-x-2;
(2)、直线AB与x轴的交点C(-2,0);
![]()
(3)、x<-4或0<x<2


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(![]() ,0),B(0,2),则点B2017的坐标为 .
,0),B(0,2),则点B2017的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
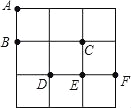
【题目】在3×3的方格纸中,点A、B、C、D、E、F分别位于如图所示的小正方形的顶点上.
(1)从A、D、E、F四个点中任意取一点,以所取的这一点及点B、C为顶点画三角形,则所画三角形是等腰三角形的概率是 ;
(2)从A、D、E、F四个点中先后任意取两个不同的点,以所取的这两点及点B、C为顶点画四边形,求所画四边形是平行四边形的概率是 (用树状图或列表法求解).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,在等腰直角三角形和含有30°角的直角三角形中,三边之间的比例关系分别如图所示:
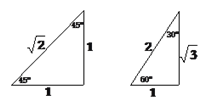
试借助上述结论,构造图形,解决下面的问题:
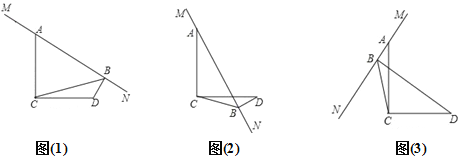
如图(1),已知∠ACD=90°,MN是过点A的直线,AC=DC,DB⊥MN于点B,
(1) 求证: BD+AB=![]() CB;
CB;
(2) 当MN绕A旋转到如图(2)和图(3)两个位置时,BD、AB、CB满足什么样关系式,请写出你的猜想,并对图(3)给予证明;
(3) MN在绕点A旋转过程中,当∠BCD=30°,BD=![]() 时,则CD= ,CB= .
时,则CD= ,CB= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com