
【题目】教室里有4排日光灯,每排灯各由一个开关控制,但灯的排数序号与开关序号不一定对应,其中控制第二排灯的开关已坏(闭合开关时灯也不亮).
(1)将4个开关都闭合时,教室里所有灯都亮起的概率是;
(2)在4个开关都闭合的情况下,不知情的雷老师准备做光学实验,由于灯光太强,他需要关掉部分灯,于是随机将4个开关中的2个断开,请用列表或画树状图的方法,求恰好关掉第一排与第三排灯的概率.
【答案】
(1)0
(2)解:用1、2、3、4分别表示第一排、第二排、第三排和第四排灯,
画树状图为:
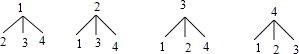
共有12种等可能的结果数,其中恰好关掉第一排与第三排灯的结果数为2,
所以恰好关掉第一排与第三排灯的概率= ![]() =
= ![]()
【解析】解:(1)因为控制第二排灯的开关已坏(闭合开关时灯也不亮,所以将4个开关都闭合时,所以教室里所有灯都亮起的概率是0;
故答案为0;
(1)由于控制第二排灯的开关已坏,所以所有灯都亮起为不可能事件;(2)用1、2、3、4分别表示第一排、第二排、第三排和第四排灯,画树状图展示所有12种等可能的结果数,再找出关掉第一排与第三排灯的结果数,然后根据概率公式求解.本题考查了列表法与树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.


科目:初中数学 来源: 题型:
【题目】王杰同学在解决问题“已知A、B两点的坐标为A(3,﹣2)、B(6,﹣5)求直线AB关于x轴的对称直线A′B′的解析式”时,解法如下:先是建立平面直角坐标系(如图),标出A、B两点,并利用轴对称性质求出A′、B′的坐标分别为A′(3,2),B′(6,5);然后设直线A′B′的解析式为y=kx+b(k≠0),并将A′(3,2)、B′(6,5)代入y=kx+b中,得方程组 ![]() ,解得
,解得 ![]() ,最后求得直线A′B′的解析式为y=x﹣1.则在解题过程中他运用到的数学思想是( )
,最后求得直线A′B′的解析式为y=x﹣1.则在解题过程中他运用到的数学思想是( ) 
A.分类讨论与转化思想
B.分类讨论与方程思想
C.数形结合与整体思想
D.数形结合与方程思想
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,等腰Rt△ABC和等腰Rt△DEF中,∠BCA=∠FDE=90°,AB=4![]() ,EF=8
,EF=8![]() .点A、C、D、E在一条直线上,等腰Rt△DEF静止不动,初始时刻,C与D重合,之后等腰Rt△ABC从C出发,沿射线CE方向以每秒1个单位长度的速度匀速运动,当A点与E点重合时,停止运动.设运动时间为t秒(t≥0).
.点A、C、D、E在一条直线上,等腰Rt△DEF静止不动,初始时刻,C与D重合,之后等腰Rt△ABC从C出发,沿射线CE方向以每秒1个单位长度的速度匀速运动,当A点与E点重合时,停止运动.设运动时间为t秒(t≥0).
(1)直接写出线段AC、DE的长度;
(2)在等腰Rt△ABC的运动过程中,设等腰Rt△ABC和等腰Rt△DEF重叠部分的面积为S,请直接写出S与t的函数关系式和相应的自变量t的取值范围;
(3)在整个运动过程中,当线段AB与线段EF相交时,设交点为点M,点O为线段CE的中点;是否存在这样的t,使点E、O、M三点构成的三角形是等腰三角形?若存在,求出对应的t的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星期六早晨蕊蕊妈妈从家里出发去观山湖公园锻炼,她连续、匀速走了60min后回家,图中的折线段OA﹣AB﹣BC是她出发后所在位置离家的距离s(km)与行走时间t(min)之间的函数关系,则下列图形中可以大致描述蕊蕊妈妈行走的路线是( ) 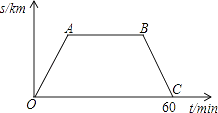
A.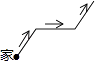
B.
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:
①∠1=∠2;②BE=CF;③△CAN≌△ABM;④CD=DN其中正确的结论是( )

A. ①② B. ②③ C. ①②③ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形OBCD的边OB在x轴上,反比例函数y= ![]() (x>0)的图象经过菱形对角线的交点A,且与边BC交于点F,点A的坐标为(4,2).
(x>0)的图象经过菱形对角线的交点A,且与边BC交于点F,点A的坐标为(4,2). 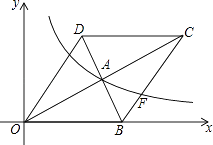
(1)求反比例函数的表达式;
(2)求点F的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com