
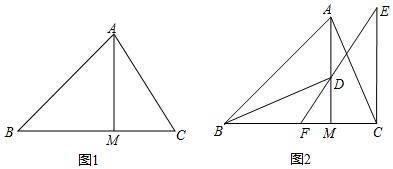
分析 (1)先由AM=BM=ABcos45°=3可得CM=2,再由勾股定理可得AC的长;
(2)延长EF到点G,使得FG=EF,证△BMD≌△AMC得AC=BD,再证△BFG≌△CFE可得BG=CE,∠G=∠E,从而得BD=BG=CE,即可得∠BDG=∠G=∠E.
解答 解:(1)∵∠ABM=45°,AM⊥BM,
∴AM=BM=ABcos45°=3$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=3,
则CM=BC-BM=5-3=2,
∴AC=$\sqrt{A{M}^{2}+C{M}^{2}}$=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$;
(2)延长EF到点G,使得FG=EF,连接BG.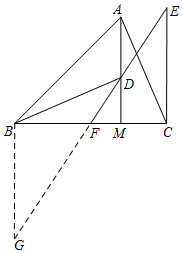
由DM=MC,∠BMD=∠AMC,BM=AM,
∴△BMD≌△AMC(SAS),
∴AC=BD,
又CE=AC,
因此BD=CE,
由BF=FC,∠BFG=∠EFC,FG=FE,
∴△BFG≌△CFE,
故BG=CE,∠G=∠E,
所以BD=CE=BG,
因此∠BDG=∠G=∠E.
点评 本题主要考查全等三角形的判定与性质及勾股定理、等腰直角三角形的性质等知识点,熟练掌握全等三角形的判定与性质是解题的关键.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:选择题
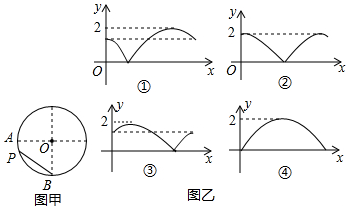
| A. | ① | B. | ③ | C. | ②或④ | D. | ①或③ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
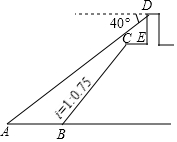 如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).
如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).| A. | 5.1米 | B. | 6.3米 | C. | 7.1米 | D. | 9.2米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com