
证明:对于任意正整数n,2n+4-2n都能被30整除
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

| 2 |
| 105 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:022
下列命题中能用举反例来证明的有________(填序号).
A.等腰三角形一定是锐角三角形;
B.等腰三角形腰长一定大于底边长;
C.等腰三角形两个底角一定是锐角;
D.顶角相等的两个等腰三角形必全等;
E.对于任意正整数a、b都有等式![]() 成立;
成立;
F.关于x的一元一次方程ax-1=0的解是 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:044
判断下列命题的真假,并给出证明:
(1)水沸腾时的温度是100℃;
(2)代数式5n+10 000的值一定比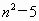 大;
大;
(3)当n=1、2、3、4时,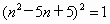 ,则对于任意正整数n,代数式
,则对于任意正整数n,代数式 的值都为1.
的值都为1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com