

分析 (1)过O作OF⊥BD于F,如图1,利用垂径定理得到BF=CF=$\frac{BC}{2}$=$\frac{x}{2}$,再利用正切的定义得到OF=x,然后证明△OFD∽△ABD,于是利用相似比可得到y与x的关系式;
(2)先利用勾股定理计算出OB=$\frac{\sqrt{5}}{2}$x,再证明△DEC∽△DCO,利用相似比可得到OD=$\frac{\sqrt{5}}{2}$y,则根据勾股定理得到x2+(y+$\frac{1}{2}$x)2=($\frac{\sqrt{5}}{2}$y)2,所以y=5x或y=-x(舍去),则$\frac{2{x}^{2}-5x}{10-2x}$=5x,然后解方程求出x即可;
(3)讨论:当OA=OB时,点A在⊙O上,如图2,根据圆周角定理得到AC为直径,即点D与点C重合,易得x=$\frac{5}{2}$,于是得到此时tan∠ADB=2;当AO=AB=5,如图3,作OH⊥AB于H,易得四边形OFBH为矩形,则OH=BF=$\frac{1}{2}$x,BH=OF=x,利用勾股定理得到(x-5)2+($\frac{1}{2}$x)2=52,然后解方程求出x,则可得到tan∠AOH=$\frac{3}{4}$,再证明∠ADB=∠AOH,从而得到tan∠ADB的值.
解答 解:(1)过O作OF⊥BD于F,如图1,则BF=CF=$\frac{BC}{2}$=$\frac{x}{2}$,
∴DF=y+$\frac{x}{2}$,
在Rt△BFO中,∵tan∠OBM=$\frac{OF}{BF}$=2,
∴OF=x,
∵AB⊥BM,
∴OF∥AB,
∴△OFD∽△ABD,
∴$\frac{OF}{AB}$=$\frac{DF}{DB}$,即$\frac{x}{5}$=$\frac{y+\frac{x}{2}}{x+y}$,
∴y=$\frac{2{x}^{2}-5x}{10-2x}$($\frac{5}{2}$<x<5);
(2)在Rt△OBF中,OB=$\sqrt{{x}^{2}+(\frac{1}{2}x)^{2}}$=$\frac{\sqrt{5}}{2}$x,
∵BC=CE,
而OB=OC=OE,
∴△OBC和△OCD为全等的等腰三角形,
∴∠OCB=∠OEC,
∴∠OCD=∠CED,
而∠CDE=∠ODC,
∴△DEC∽△DCO,
∴$\frac{CE}{OC}$=$\frac{CD}{OD}$,即$\frac{x}{\frac{\sqrt{5}x}{2}}$=$\frac{y}{OD}$,
∴OD=$\frac{\sqrt{5}}{2}$y,
在Rt△OFD中,∵OF2+FD2=OD2,
∴x2+(y+$\frac{1}{2}$x)2=($\frac{\sqrt{5}}{2}$y)2,
整理得y2-4xy-5x2=0,
∴y=5x或y=-x(舍去),
∴$\frac{2{x}^{2}-5x}{10-2x}$=5x,解得x1=0(舍去),x2=$\frac{55}{12}$,
即BC的长为$\frac{55}{12}$;
(3)当OA=OB时,点A在⊙O上,如图2,则AC为直径,点D与点C重合,OF=$\frac{1}{2}$AB,即x=$\frac{5}{2}$,
∴tan∠ADB=$\frac{5}{\frac{5}{2}}$=2;
当AO=AB=5,如图3,作OH⊥AB于H,易得四边形OFBH为矩形,
∴OH=BF=$\frac{1}{2}$x,BH=OF=x,
在Rt△OHA中,∵AH2+OH2=OA2,
∴(x-5)2+($\frac{1}{2}$x)2=52,
解得x1=0(舍去),x2=8,
∴tan∠AOH=$\frac{AH}{OH}$=$\frac{8-5}{4}$=$\frac{3}{4}$,
∵OH∥BD,
∴∠ADB=∠AOH,
∴tan∠ADB=$\frac{3}{4}$.
点评 本题考查了圆的综合题:熟练掌握垂径定理、圆周角定理和等腰三角形的性质;会应用锐角三角函数和相似三角形的判定进行几何计算;学会运用分类讨论的思想解决数学问题;根据题意画出相应的几何图形是解决问题的关键.


科目:初中数学 来源: 题型:解答题
| A型销售数量(台) | B型销售数量(台) | 总利润(元) |
| 5 | 10 | 2000 |
| 10 | 5 | 2500 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
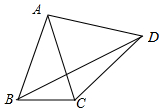 如图,△ABC中,AB=AC=5,BC=2,以AC为边在△ABC外作等边三角形ACD,连接BD,则BD=$\sqrt{3}$+2$\sqrt{6}$.
如图,△ABC中,AB=AC=5,BC=2,以AC为边在△ABC外作等边三角形ACD,连接BD,则BD=$\sqrt{3}$+2$\sqrt{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com