
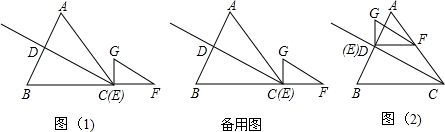
分析 (1)作高AH,根据tanB=2设BH=x,则AH=2x,CH=10-x,利用勾股定理列方程求x的值,则AH=8;
(2)分四种情形①当0<t≤$\frac{3}{2}$时,如图2中,重叠部分是△EMN.②当$\frac{3}{2}$<t≤$\frac{7}{2}$时,如图5中,重叠部分是四边形EGMN.③如图6中,当$\frac{7}{2}$<t≤4时,重叠部分是五边形EKPMN.④如图7中,当4<t≤6时,重叠部分是△PKF.分别求解即可.
(3)分两种情形①如图8中,当GF∥BC时,易证明△MAN是等腰三角形.②如图9中,当DG∥AC时,易证明△ANM是等腰三角形,MA=MN,△MGD是等腰三角形,MG=MD.分别求出DM的长即可解决问题.
解答 解:(1)如图1,过A作AH⊥BC,垂足为H,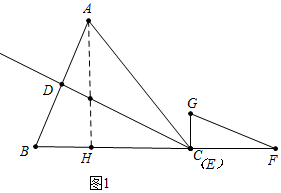
在Rt△ABH中,tan∠B=$\frac{AH}{BH}$=2,设BH=x,则AH=2x,CH=10-x,
由勾股定理得:AH2+CH2=AC2,
(2x)2+(10-x)2=102,
解得:x1=0(舍),x2=4,
∴AH=2x=8,
答:点A到BC的距离是8;
(2)①如图2中,重叠部分是△EMN.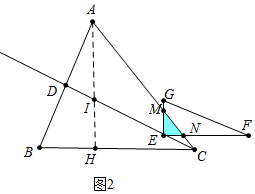
由(1)得:AH=8,BH=4,
∴CH=6,
∴AB=$\sqrt{{8}^{2}+{4}^{2}}$=4$\sqrt{5}$,
∴AD=BD=2$\sqrt{5}$,
∵∠ADI=∠IHC=90°,∠AID=∠CIH,
∴∠BAH=∠ICH,
∵∠BAH+∠B=90°,∠ICH+∠HIC=90°,
∴∠B=∠HIC,
∴tan∠HIC=tan∠B=$\frac{CH}{HI}$=2,
∴$\frac{6}{HI}$=2,
∴HI=3,
∴AI=5,由勾股定理得:DI=$\sqrt{{5}^{2}-(2\sqrt{5})^{2}}$=$\sqrt{5}$,CI=$\sqrt{{3}^{2}+{6}^{2}}$=3$\sqrt{5}$,
由题意得:CE=$\sqrt{5}$t,
∵EG∥AH,
∴$\frac{EM}{AI}=\frac{CE}{CI}$,
∴$\frac{EM}{5}=\frac{\sqrt{5}t}{3\sqrt{5}}$,
∴EM=$\frac{5}{3}$t,tan∠EMN=tan∠HAC=$\frac{EN}{EM}=\frac{CH}{AH}$,
∴$\frac{EN}{\frac{5}{3}t}$=$\frac{6}{8}$,
∴EN=$\frac{5}{4}t$,
∴S=$\frac{1}{2}$EM•EN=$\frac{1}{2}$•$\frac{5}{3}$t•$\frac{5}{4}t$=$\frac{25}{24}{t}^{2}$,
如图3,当G落在AC上时,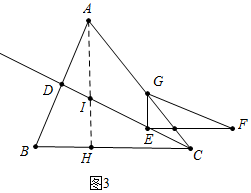
EG=$\frac{5}{3}$t=$\frac{5}{2}$,t=$\frac{3}{2}$;∴当0<t≤$\frac{3}{2}$时,S=$\frac{25}{24}{t}^{2}$;
②如图4中,当G在AB上时,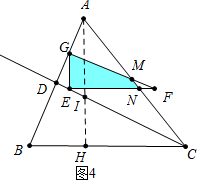
∵EG∥AI,
∴$\frac{EG}{AI}$=$\frac{ED}{DI}$,
∴$\frac{\frac{5}{2}}{5}$=$\frac{DE}{\sqrt{5}}$,
∴DE=$\frac{\sqrt{5}}{2}$,
∴CE=$\frac{7}{2}$$\sqrt{5}$=$\sqrt{5}$t,
∴t=$\frac{7}{2}$,
∴当$\frac{3}{2}$<t≤$\frac{7}{2}$时,如图5中,重叠部分是四边形EGMN,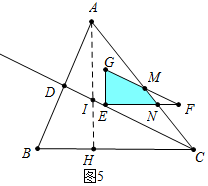
S=S△EFG-S△MNF=$\frac{25}{4}$-($\frac{5}{8}$t2-5t+10)=-$\frac{5}{8}$t2+5t-$\frac{15}{4}$.
③如图6中,当$\frac{7}{2}$<t≤4时,重叠部分是五边形EKPMN.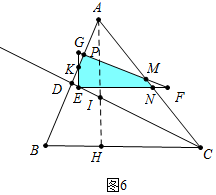
S=S△GEF-S△PGK-S△MNF=$\frac{25}{4}$-5(t-$\frac{7}{2}$)2-($\frac{5}{8}$t2-5t+10)=-$\frac{45}{8}$t2+40t-65.
④如图7中,当4<t≤6时,重叠部分是△PKF.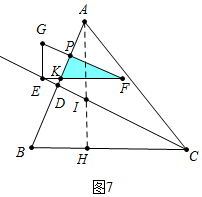
S=$\frac{1}{2}$•PK•PF=$\frac{1}{2}$•($\sqrt{5}$-$\frac{\sqrt{5}t-4\sqrt{5}}{2}$)•2($\sqrt{5}$-$\frac{\sqrt{5}t-4\sqrt{5}}{2}$)=$\frac{5}{4}$t2-15t+45.
综上所述,S=$\left\{\begin{array}{l}{\frac{25}{24}{t}^{2}}&{(0<t≤\frac{3}{2})}\\{-\frac{5}{8}{t}^{2}+5t-\frac{15}{4}}&{(\frac{3}{2}<t≤\frac{7}{2})}\\{-\frac{45}{8}{t}^{2}+40t-65}&{(\frac{7}{2}<t≤4)}\\{\frac{5}{4}{t}^{2}-15t+45}&{(4<t≤6)}\end{array}\right.$.
(3)①如图8中,当GF∥BC时,易证明△MAN是等腰三角形,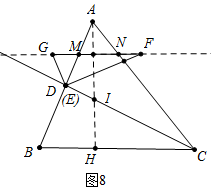
∵MN=AN,
∴∠A=∠NMA=∠G,
∴DG=DM=$\frac{5}{2}$,
∴AM=AD-DM=2$\sqrt{5}$-$\frac{5}{2}$.
②如图9中,当DG∥AC时,易证明△ANM是等腰三角形,MA=MN,△MGD是等腰三角形,MG=MD,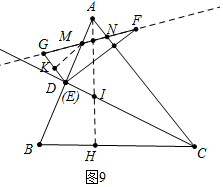
作MK⊥GD于K.
∵MG=MD,MK⊥GD,
∴KD=KG=$\frac{5}{4}$,MK=2KD=$\frac{5}{2}$,
ME=$\frac{5}{4}$$\sqrt{5}$,
∴AM=AD-MD=2$\sqrt{5}$-$\frac{5}{4}$$\sqrt{5}$=$\frac{3}{4}$$\sqrt{5}$.
点评 本题考查平移变换、旋转变换、等腰三角形的性质、勾股定理、三角形面积等知识,解题的关键是学会正确画出图形,确定自变量x的取值范围,学会利用分段函数表示函数关系式,学会分类讨论的思想思考问题,题目比较复杂,计算量比较大,属于中考压轴题.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
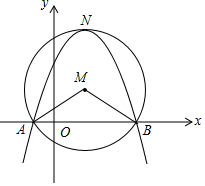 如图,在平面直角坐标系中,O是原点,以点M(2,2)为圆心,4为半径作圆,交x轴于A,B两点,开口向下的抛物线经过点A,B,且其顶点N在⊙M上.
如图,在平面直角坐标系中,O是原点,以点M(2,2)为圆心,4为半径作圆,交x轴于A,B两点,开口向下的抛物线经过点A,B,且其顶点N在⊙M上.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
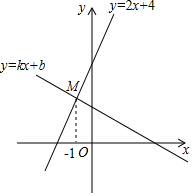 如图,已知直线y=2x+4与直线y=kx+b交于点M(-1,a),则关于x,y的二元一次方程组$\left\{\begin{array}{l}{2x-y+4=0}\\{kx-y+b=0}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$.
如图,已知直线y=2x+4与直线y=kx+b交于点M(-1,a),则关于x,y的二元一次方程组$\left\{\begin{array}{l}{2x-y+4=0}\\{kx-y+b=0}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
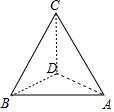 如图,为了估测某塔的高度,在同一水平面的A,B两点处进行测量.在点A处测得塔顶C在西偏北20°的方向上,仰角为60°;在点B处侧得塔顶C在东偏北40°的方向上,仰角为30°,若A,B两点相距130m,则塔的高度CD=10$\sqrt{39}$m.
如图,为了估测某塔的高度,在同一水平面的A,B两点处进行测量.在点A处测得塔顶C在西偏北20°的方向上,仰角为60°;在点B处侧得塔顶C在东偏北40°的方向上,仰角为30°,若A,B两点相距130m,则塔的高度CD=10$\sqrt{39}$m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
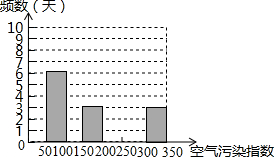 根据国家环保局统一规定,我国空气质量分为5个等级,当空气污染指数达到0-50时为1级;51-100时为2级,101-200时为3级;201-300时为4级;300以上时为5级,其中3级属于轻度污染,4级属于中度污染,5级属于重度污染.某城市环保局随机抽取了2013年某些天的空气质量检测数据,并整理绘制成如图频数分布表和频数分布直方图.
根据国家环保局统一规定,我国空气质量分为5个等级,当空气污染指数达到0-50时为1级;51-100时为2级,101-200时为3级;201-300时为4级;300以上时为5级,其中3级属于轻度污染,4级属于中度污染,5级属于重度污染.某城市环保局随机抽取了2013年某些天的空气质量检测数据,并整理绘制成如图频数分布表和频数分布直方图.| 空气污染指数 | 频数(天) | 频率 |
| 50<x≤100 | 6 | 0.2 |
| 100<x≤150 | a | 0.3 |
| 150<x≤200 | 3 | 0.1 |
| 200<x≤250 | 6 | 0.2 |
| 250<x≤300 | b | c |
| 300<x≤350 | 3 | 0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
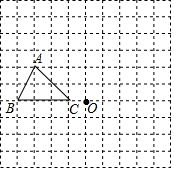 在如图的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC顶点都在格点上(每个小方格的顶点叫格点).
在如图的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC顶点都在格点上(每个小方格的顶点叫格点).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
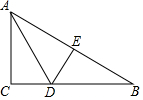 如图,△ABC中∠C=90°,线段AD是△ABC的角平分线,直线DE是线段AB的垂直平分线.若DE=1cm,DB=2cm,AC=$\sqrt{3}$cm.求点C到直线AD的距离.
如图,△ABC中∠C=90°,线段AD是△ABC的角平分线,直线DE是线段AB的垂直平分线.若DE=1cm,DB=2cm,AC=$\sqrt{3}$cm.求点C到直线AD的距离.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com