
【题目】如图1,已知抛物线y=ax2+bx+3=0(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C
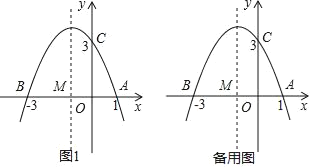
(1)求抛物线的解析式;
(2)设抛物线的对称轴与x轴交于点M,请问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由;
(3)在抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
【答案】(1)y=﹣x2﹣2x+3;(2)存在符合条件的点P,其坐标为![]() 或
或![]() 或(﹣1,6)或
或(﹣1,6)或![]() ;(3)存在,Q(﹣1,2).
;(3)存在,Q(﹣1,2).
【解析】
(1)已知抛物线过A、B两点,可将两点的坐标代入抛物线的解析式中,用待定系数法即可求出二次函数的解析式;
(2)可根据(1)的函数解析式得出抛物线的对称轴,也就得出了M点的坐标,由于C是抛物线与y轴的交点,因此C的坐标为(0,3),根据M、C的坐标可求出CM的距离.然后分三种情况进行讨论:
①当CP=PM时,②当CM=MP时,③当CM=CP时,可分别得出P的坐标;
(3)根据轴对称﹣最短路径问题解答.
解:(1)∵抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),
∴![]() ,
,
解得:![]() .
.
∴所求抛物线解析式为:y=﹣x2﹣2x+3;
(2)存在,如图1,
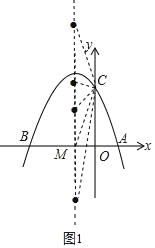
∵抛物线解析式为:y=﹣x2﹣2x+3,
∴其对称轴为![]() ,
,
∴设P点坐标为(﹣1,a),
∴C(0,3),M(﹣1,0),
PM2=a2,CM2=(﹣1)2+32,CP2=(﹣1)2+(3﹣a)2,
分类讨论:
(1)当PC=PM时,
(﹣1)2+(3﹣a)2=a2,解得![]() ,
,
∴P点坐标为:P1(﹣1,![]() );
);
(2)当MC=MP时,
(﹣1)2+32=a2,解得![]() ,
,
∴P点坐标为:![]() 或
或![]() ;
;
(3)当CM=CP时,
(﹣1)2+32=(﹣1)2+(3﹣a)2,解得a=6,a=0(舍),
∴P点坐标为:P4(﹣1,6).
综上所述存在符合条件的点P,其坐标为![]() 或
或![]() 或P(﹣1,6)或
或P(﹣1,6)或![]() .
.
(3)存在,Q(﹣1,2),
理由如下:如图2,
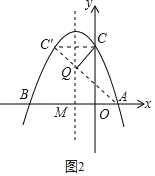
点C(0,3)关于对称轴x=﹣1的对称点C′的坐标是(﹣2,3),连接AC′,直线AC′与对称轴的交点即为点Q.
设直线AC′函数关系式为:y=kx+t(k≠0).
将点A(1,0),C′(﹣2,3)代入,得![]() ,
,
解得![]() ,
,
所以,直线AC′函数关系式为:y=﹣x+1.
将x=﹣1代入,得y=2,即Q(﹣1,2).


 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
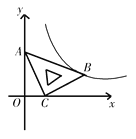
【题目】在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),AB=![]() ,点A在y轴上,反比例函数经过点B,求反比例函数解析式______.
,点A在y轴上,反比例函数经过点B,求反比例函数解析式______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把有一条边是另一条边的2倍的梯形叫做“倍边梯形”,在⊙O中,直径AB=2,PQ是弦,若四边形ABPQ是“倍边梯形”,那么PQ的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
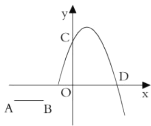
【题目】如图,已知![]() ,线段
,线段![]() 与
与![]() 轴平行,且
轴平行,且![]() ,抛物线
,抛物线![]() 经过点
经过点![]() 和
和![]() ,若线段
,若线段![]() 以每秒2个单位长度的速度向下平移,设平移的时间为
以每秒2个单位长度的速度向下平移,设平移的时间为![]() (秒).若抛物线与线段
(秒).若抛物线与线段![]() 有公共点,则
有公共点,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①BE⊥AC;②四边形BEFG是平行四边形;③△EFG≌△GBE;④EG=EF,其中正确的个数是( )
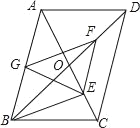
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】风电已成为我国继煤电、水电之后的第三大电源,风电机组主要由塔杆和叶片组成(如图1),图2是从图1引出的平面图.假设你站在A处测得塔杆顶端C的仰角是55°,沿HA方向水平前进43米到达山底G处,在山顶B处发现正好一叶片到达最高位置,此时测得叶片的顶端D(D、C、H在同一直线上)的仰角是45°.已知叶片的长度为35米(塔杆与叶片连接处的长度忽略不计),山高BG为10米,BG⊥HG,CH⊥AH,求塔杆CH的高.(参考数据:tan55°≈1.4,tan35°≈0.7,sin55°≈0.8,sin35°≈0.6)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我国新型冠状病毒防控形势好转的态势下,各行各业复工复产所需的“消杀防护”设备成为急需物品.某医药超市库存的甲,乙两种型号“消杀防护”套装共![]() 套全部售完,售后统计甲型号套装每套的利润为
套全部售完,售后统计甲型号套装每套的利润为![]() 元,乙型号套装每套的利润为
元,乙型号套装每套的利润为![]() 元,两种型号“消杀防护"套装售完后的总利润为
元,两种型号“消杀防护"套装售完后的总利润为![]() 元
元
![]() 请计算本次销售中甲、乙两种型号“消杀防护”套装各销售了多少套.
请计算本次销售中甲、乙两种型号“消杀防护”套装各销售了多少套.
![]() 由于企业迫切需求,该医药超市决定再次购进
由于企业迫切需求,该医药超市决定再次购进![]() 套甲、乙两种型号的“消杀防护”套装,商场规定甲型号套装的采购数量不得超过乙型号的
套甲、乙两种型号的“消杀防护”套装,商场规定甲型号套装的采购数量不得超过乙型号的![]() 倍,请你通过计算说明如何采购才能让第二次销售获得最大利润.
倍,请你通过计算说明如何采购才能让第二次销售获得最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程:2(x﹣k)=x﹣4①和关于x的一元二次方程:(k﹣1)x2+2mx+(3﹣k)+n=0②(k、m、n均为实数),方程①的解为非正数.
(1)求k的取值范围;
(2)如果方程②的解为负整数,k﹣m=2,2k﹣n=6且k为整数,求整数m的值;
(3)当方程②有两个实数根x1、x2,满足(x1+x2)(x1﹣x2)+2m(x1﹣x2+m)=n+5,且k为正整数,试判断|m|≤2是否成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某快递公司每天上午9:00-10:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为__________;
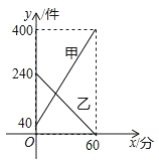
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com