
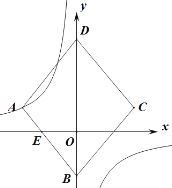
【题目】如图,菱形ABCD的顶点A在反比例函数![]() 的图象上,B(0,-5)、D在
的图象上,B(0,-5)、D在![]() 轴上,点E(-4,0)是
轴上,点E(-4,0)是![]() 与x轴的交点,若菱形ABCD面积
与x轴的交点,若菱形ABCD面积![]() ,则k值为( )
,则k值为( )
A.-36B.-16C.![]() D.-24
D.-24
科目:初中数学 来源: 题型:
【题目】某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)求出y与x的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,P是抛物线y=-x2+3x上一点,且在x轴上方,过点P分别向x轴、y轴作垂线,得到矩形PMON.若矩形PMON的周长随点P的横坐标m增大而增大,则m的取值范围是_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在初中阶段的函数学习中,我们经历了“确定函数的表达式--利用函数图象研究其性质--运用函数解决问题”的学习过程.在画函数图象时,我们通过描点连线或平移的方法画出函数图象.结合上面经历的学习过程,我们来解决下面的问题:已知函数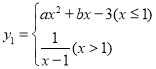 .
.
(1)当x=-1时,![]() =0;当x=-2时,
=0;当x=-2时,![]() =5,则
=5,则![]() = ,
= ,![]() = .
= .
(2)在给出的平面直角坐标系中画出该函数图像
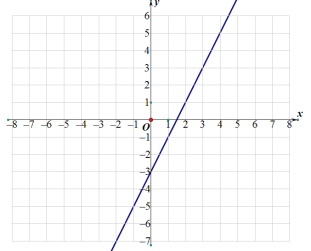
(3)已知函数![]() 的图像如图所示,结合你画出的函数图像,直接写出
的图像如图所示,结合你画出的函数图像,直接写出![]() 时,x的取值范围
时,x的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,如果每次发出的乒乓球的运动路线固定不变,且落在中线上,在乒乓球从发射出到第一次落在桌面的运行过程中,设乒乓球与端点A的水平距离为x(米),距桌面的高度为y(米),运行时间为t(秒),经多次测试后,得到如下部分数据:
t(秒) | 0 | 0.16 | 0.2 | 0.4 | 0.6 | 0.64 | 0.8 | … |
x(米) | 0 | 0.4 | 0.5 | 1 | 1.5 | 1.6 | 2 | … |
y(米) | 0.25 | 0.378 | 0.4 | 0.45 | 0.4 | 0.378 | 0.25 | … |
(1)如果y是t的函数,
①如图,在平面直角坐标系tOy中,描出了上表中y与t各对对应值为坐标的点.请你根据描出的点,画出该函数的图象;
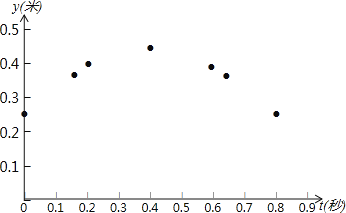
②当t为何值时,乒乓球达到最大高度?
(2)如果y是关于x的二次函数,那么乒乓球第一次落在桌面时,与端点A的水平距离是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
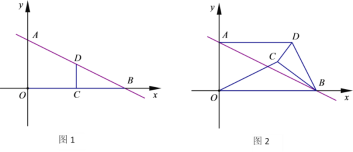
【题目】如图,在平面直角坐标系中,直线l:![]() 与x轴.y轴交于B,A两点,点D,C分别为线段AB,OB的中点,连结CD,如图,将△DCB绕点B按顺时针方向旋转角
与x轴.y轴交于B,A两点,点D,C分别为线段AB,OB的中点,连结CD,如图,将△DCB绕点B按顺时针方向旋转角![]() ,如图.
,如图.
(1)连结OC,AD,求证![]() ∽
∽![]() ;
;
(2)当0°<![]() <180°时,若△DCB旋转至A,C,D三点共线时,求线段OD的长;
<180°时,若△DCB旋转至A,C,D三点共线时,求线段OD的长;
(3)试探索:180°<![]() <360°时,是否还有可能存在A,C,D三点共线的情况,若存在,求出此直线的表达式;若不存在,请说明理由.
<360°时,是否还有可能存在A,C,D三点共线的情况,若存在,求出此直线的表达式;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com