
【题目】有这样一个问题,如图1,在等边![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的动点,且
上的动点,且![]() ,若
,若![]() ,试求
,试求![]() 的长.爱钻研的小峰同学发现,可以通过几何与函数相结合的方法来解决这个问题,下面是他的探究思路,请帮他补充完整.
的长.爱钻研的小峰同学发现,可以通过几何与函数相结合的方法来解决这个问题,下面是他的探究思路,请帮他补充完整.
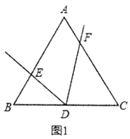
(1)注意到![]() 为等边三角形,且
为等边三角形,且![]() ,可得
,可得![]() ,于是可证
,于是可证![]() ,进而可得
,进而可得![]() ,注意到
,注意到![]() 为
为![]() 中点,
中点,![]() ,因此
,因此![]() 和
和![]() 满足的等量关系为______.
满足的等量关系为______.
(2)设![]() ,
,![]() ,则
,则![]() 的取值范围是______.结合(1)中的关系求
的取值范围是______.结合(1)中的关系求![]() 与
与![]() 的函数关系.
的函数关系.
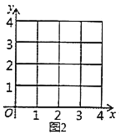
(3)在平面直角坐标系![]() 中,根据已有的经验画出
中,根据已有的经验画出![]() 与
与![]() 的函数图象,请在图2中完成画图.
的函数图象,请在图2中完成画图.
(4)回到原问题,要使![]() ,即为
,即为![]() ,利用(3)中的图象,通过测量,可以得到原问题的近似解为
,利用(3)中的图象,通过测量,可以得到原问题的近似解为![]() ______(精确到0.1)
______(精确到0.1)
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中四边形OABC是边长为6的正方形,平行于对角线AC的直线l从O出发,沿x轴正方向以每秒一个单位长度的速度运动,运动到直线l与正方形没有交点为止,设直线l扫过正方形OABC的面积为S,直线l的运动时间为t(秒),下列能反映S与t之间的函数图象的是( )
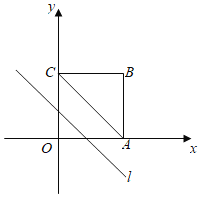
A. B.
B.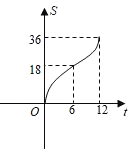
C.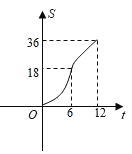 D.
D.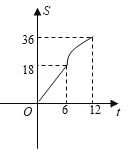
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,且AB为⊙O的直径.∠ACB的平分线CD交⊙O于点D,过点D作⊙O的切线PD交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.
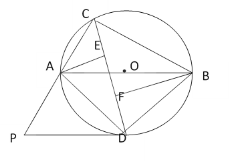
(1)求证:DP∥AB;
(2)试猜想线段AE、EF、BF之间的数量关系,并加以证明;
(3)若AC=6,BC=8,求线段PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ABC=90°,∠BAC=30°,将△ABC绕点A顺时针旋转一定的角度![]() 得到△AED,点B、C的对应点分别是E、D.
得到△AED,点B、C的对应点分别是E、D.
(1)如图1,当点E恰好在AC上时,求∠CDE的度数;
(2)如图2,若![]() =60°时,点F是边AC中点,求证:四边形BFDE是平行四边形.
=60°时,点F是边AC中点,求证:四边形BFDE是平行四边形.


查看答案和解析>>
科目:初中数学 来源: 题型:
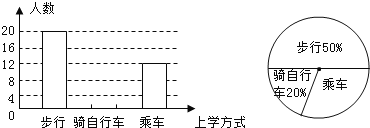
【题目】学习了统计知识后,小明的数学老师要求每个学生就本班同学的上学方式进行一次调查统计,如图是小明通过收集数据后绘制的两幅不完整的统计图. 请根据图中提供的信息,解答下列问题:
(1)该班共有_______________名学生;
(2)将“骑自行车”部分的条形统计图补充完整;
(3)在扇形统计图中;求出“乘车”部分所对应的圆心角的度数;
(4)若全年级有600名学生,试估计该年级骑自行车上学的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() 有两个实数根x1,x2.
有两个实数根x1,x2.
(1)求实数k的取值范围;
(2)是否存在实数k使得![]() 成立?若存在,请求出k的值;若不存在,请说明理由.
成立?若存在,请求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC中∠ACB=90°,E在AB上,以AE为直径的⊙O与BC相切于D,与AC相交于F,连接AD.
(1)求证:AD平分∠BAC;
(2)若DF∥AB,则BD与CD有怎样的数量关系?并证明你的结论.
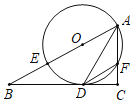
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com