解:(1)∵AB的垂直平分线为y轴,
∴OA=OB=

AB=

×2=1,
∴A的坐标是(-1,0),B的坐标是(1,0).
在直角△OAC中,OC=

=2,
则C的坐标是:(0,2);
(2)设抛物线的解析式是:y=ax
2+b,
根据题意得:
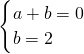
,
解得:

,
则抛物线的解析式是:y=-2x
2+2;
(3)∵S
△ABC=

AB•OC=

×2×2=2,
∴S
△ABD=

S
△ABC=1.
设D的纵坐标是m,则

AB•|m|=1,
则m=±1.
当m=1时,-2x
2+2=1,解得:x=±

,
当m=-1时,-2x
2+2=-1,解得:x=±

,
则D的坐标是:(

,1)或(-

,1)或(

,-1),或(-

,-1).
(4)设抛物线向右平移c个单位长度,则0<c≤1,OA′=1-c,OB′=1+c.
平移以后的抛物线的解析式是:y=-2(x-c)
2+b.
令x=0,解得y=-2c
2+2.即OC′=-2c
2+2.
当点C′同时在以A′B′为直径的圆上时有:OC′
2=OA′•OB′,
则(-2c
2+2)
2=(1-c)(1+c),
即(4c
2-3)(c
2-1)=0,
解得:c=

,-

(舍去),1,-1(舍去).
故平移

或1个单位长度.
分析:(1)根据y轴是AB的垂直平分线,则可以求得OA,OB的长度,在直角△OAC中,利用勾股定理求得OC的长度,则A、B、C的坐标即可求解;
(2)利用待定系数法即可求得二次函数的解析式;
(3)首先求得△ABC的面积,根据S
△ABD=

S
△ABC,以及三角形的面积公式,即可求得D的纵坐标,把D的纵坐标代入二次函数的解析式,即可求得横坐标.
(4)设抛物线向右平移c个单位长度,则0<c≤1,可以写出平移以后的函数解析式,当点C′同时在以A′B′为直径的圆上时有:OC′
2=OA′•OB′,据此即可得到一个关于c的方程求得c的值.
点评:本题考查了勾股定理,待定系数法求二次函数的解析式,以及图象的平移,正确理解:当点C′同时在以A′B′为直径的圆上时有:OC′
2=OA•OB,是解题的关键.

 如图,在△ABC中,AB=2,AC=BC=
如图,在△ABC中,AB=2,AC=BC= .
. S△ABC;
S△ABC; ,y4=-
,y4=- .
. ,y4=-
,y4=- .
. ,可设y=
,可设y= ,用同样的方法也可求解.
,用同样的方法也可求解. AB=
AB= ×2=1,
×2=1, =2,
=2,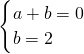 ,
, ,
, AB•OC=
AB•OC= ×2×2=2,
×2×2=2, S△ABC=1.
S△ABC=1. AB•|m|=1,
AB•|m|=1, ,
, ,
, ,1)或(-
,1)或(- ,1)或(
,1)或( ,-1),或(-
,-1),或(- ,-1).
,-1). ,-
,- (舍去),1,-1(舍去).
(舍去),1,-1(舍去). 或1个单位长度.
或1个单位长度. S△ABC,以及三角形的面积公式,即可求得D的纵坐标,把D的纵坐标代入二次函数的解析式,即可求得横坐标.
S△ABC,以及三角形的面积公式,即可求得D的纵坐标,把D的纵坐标代入二次函数的解析式,即可求得横坐标.

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为