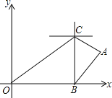
【题目】在一次数学活动中，李明利用一根栓有小锤的细线和一个半圆形量角器制作了一个测角仪，去测量学校内一座假山的高度CD．如图，已知小明距假山的水平距离BD为12m，他的眼镜距地面的高度为1.6m，李明的视线经过量角器零刻度线OA和假山的最高点C，此时，铅垂线OE经过量角器的60°刻度线，则假山的高度为【 】
A．（4
+1.6）m B．（12+1.6）m C．（4+1.6）m D．4m
口算题卡加应用题集训系列答案
综合自测系列答案科目：初中数学 来源： 题型：
【题目】在围棋盒中有 x 颗黑色棋子和 y 颗白色棋子，从盒中随机地取出一个棋子，如果它是黑色棋子的概率是
；如果往盒中再放进 10 颗黑色棋子，则取得黑色棋子的概率变为
．求 x 和 y 的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】△ABC是等腰直角三角形，点E为线段AC上一点（E点不和A、C两点重合），连接BE并延长BE，在BE的延长线上找一点D，使AD⊥CD，点F为线段AD上一点（F点不和A、D两点重合），连接CF，交BD于点G
（1）如图1，若AB＝
，CD＝1，F是线段AD的中点，求CF；
（2）如图2，若点E是线段AC中点，CF⊥BD，求证：CF+DE＝BE．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①，在△ABC中，AB=AC，D是射线BC上一点(点D不与点B重合)，连结AD，将AD绕着点D逆时针旋转∠BAC的度数得到AE，连结DE、CE.
（1）当点D在边BC上，求证：△BAD≌△CAE.
（2）当点D在边BC上，若∠BAC=a，求∠DCE的大小．(用含a的代数式表示).
（3）当DE与△ABC的边所在的直线垂直，且∠BAC=40°时，请借助图②，直接写出∠CED的大小.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①，在四边形ABCD中，AC⊥BD于点E，AB=AC=BD，点M为BC中点，N为线段AM上的点，且MB=MN.
（1）求证：BN平分∠ABE；
（2）若BD=1，连结DN，当四边形DNBC为平行四边形时，求线段BC的长；
（3）如图②，若点F为AB的中点，连结FN、FM，求证：△MFN∽△BDC.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】中国派遣三艘海监船在南海保护中国渔民不受菲律宾的侵犯．在雷达显示图上，标明了三艘海监船的坐标为
、
、
，（单位：海里）三艘海监船安装有相同的探测雷达，雷达的有效探测范围是半径为
的圆形区域（只考虑在海平面上的探测）．
若在三艘海监船组成的
区域内没有探测盲点，则雷达的有效探测半径至少为________海里；
某时刻海面上出现一艘菲律宾海警船
，在海监船
测得点位于南偏东
方向上，同时在海监船
测得位于北偏东
方向上，海警船正以每小时
海里的速度向正西方向移动，我海监船立刻向北偏东
方向运动进行拦截，问我海监船至少以多少速度才能在此方向上拦截到菲律宾海警船？
查看答案和解析>>
科目：初中数学 来源： 题型：
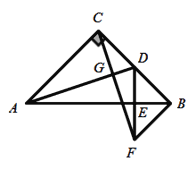
【题目】如图，在等腰
中，
，D为BC的中点，过点C作
于点G，过点B作
于点B，交CG的延长线于点F，连接DF交AB于点E.
(1)求证：
；
(2)求证：AB垂直平分DF；
(3)连接AF，试判断
的形状，并说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在初中阶段的函数学习中，我们经历了“确定函数的表达式——利用函数图象研究其性质——运用函数解决问题”的学习过程. 在画函数图象时，我们通过描点、平移、对称的方法画出了所学的函数图象. 同时，我们也学习了绝对值的意义
，结合上面经历的学习过程，现在来解决下面的问题
在函数
中，自变量
的取值范围是全体实数，下表是
与的几组对应值：
|
| 0 | 1 | 2 | 3 | ||
y | … | 0 | 1 | 2 | 3 | 2 | … |
(1)根据表格填写：
_______.
(2)化简函数解析式：
当
时，
_______；
当
时，______.
(3)在给出的平面直角坐标系中，请用你喜欢的方法画出这个函数的图象并解决以下问题；
①该函数的最大值为_______.
②若
为该函数图象上不同的两点，则
________.
③根据图象可得关于的方程
的解为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
