

分析 (1)根据线段的和差,可得答案;
(2)①根据正方形的面积公式,②根据面积的和差,可得答案;
(3)根据面积相等,可得答案;
(4)根据间接求面积的方法,可得答案.
解答 解:(1)你认为图②中的阴影部分的正方形的边长等于 m-n
(2)请你用两种不同的方式列代数式表示图②中阴影部分的面积.
方法①(m-n)2
方法②(m+n)2-4mn
(3)观察图②,写出(m+n)2,(m-n)2,mn这三个代数式之间的等量关系:(m-n)2=(m+n)2-4mn,
故答案为:m-n;(m-n)2,(m+n)2-4mn;(m-n)2=(m+n)2-4mn;
(4)(m-n)2=(m+n)2-4mn=52-4×4=9,
m-n=3.
点评 本题考查了完全平方公式,利用(m-n)2=(m+n)2-4mn是解题关键.


科目:初中数学 来源: 题型:解答题
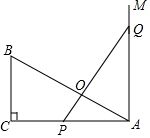 如图,已知△ABC是直角三角形,∠C=90°,AC=10cm,BC=5cm,射线AM⊥AC,点P在AC上运动(不与点A,C重合),点Q在AM上运动(不与点A重合),且始终保持PQ=AB.
如图,已知△ABC是直角三角形,∠C=90°,AC=10cm,BC=5cm,射线AM⊥AC,点P在AC上运动(不与点A,C重合),点Q在AM上运动(不与点A重合),且始终保持PQ=AB.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
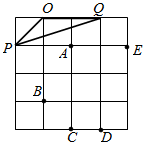 如图,△OPQ在边长为1个单位的方格纸中,它们的顶点在小正方形顶点位置,点A,B,C,D,E也是小正方形的顶点,从点A,B,C,D,E中选取三个点所构成的三角形与△OPQ相似,那么这个三角形是△CDB.
如图,△OPQ在边长为1个单位的方格纸中,它们的顶点在小正方形顶点位置,点A,B,C,D,E也是小正方形的顶点,从点A,B,C,D,E中选取三个点所构成的三角形与△OPQ相似,那么这个三角形是△CDB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +1 | +1.2 | -1 | +2 | -1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
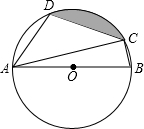 如图,四边形ABCD是⊙O的内接四边形,AB是⊙O的直径,∠D=108°,连接AC.
如图,四边形ABCD是⊙O的内接四边形,AB是⊙O的直径,∠D=108°,连接AC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com