
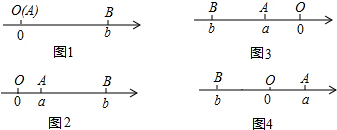
分析 ①根据两点间的距离公式即可求解;
②根据两点间的距离公式可求数轴上表示x和-1的两点A和B之间的距离,再根据两点间的距离公式列出方程可求x;
③求|x+1|+|x-2|的最小值,意思是x到-1的距离之和与到2的距离之和最小,那么x应在-1和2之间的线段上;
④根据提示列出算式计算即可求解.
解答 解:①数轴上表示2和5两点之间的距离是:|2-5|=3,
数轴上表示-2和-5的两点之间的距离是:|-2+5|=3,
数轴上表示1和-3的两点之间的距离是:|1+3|=4,
②数轴上表示x和-1的两点A和B之间的距离是:|x+1|,
当|AB|=2,即|x+1|=2,
解得x=-3或1.
③若|x+1|+|x-2|取最小值,那么表示x的点在-1和2之间的线段上,
所以-1≤x≤2.
④解:当$x=\frac{1+2015}{2}=1008$时,|x-1|+|x-2|+|x-3|+…+|x-2015|最小,
最小值为1+2+3+…+1007+0+1+2+3+…+1007
=(1+2+3+…+1007)×2
=$\frac{(1+1007)×1007}{2}×2$
=1015056.
故答案为:3,3,4;|x+1|,-3或1;-1≤x≤2.
点评 本题考查了数轴,涉及的知识点为:数轴上两点间的距离=两个数之差的绝对值.绝对值是正数的数有2个.


 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
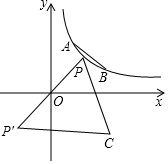 如图点A(1,2)、B(2,1)在反比例函数y=$\frac{2}{x}$图象上,点P是反比例函数y=$\frac{2}{x}$在第一象限图象上的一个动点,作点P关于原点对称的点P′,以P P′为边作等边△P P′C,点C(x,y)在第四象限.
如图点A(1,2)、B(2,1)在反比例函数y=$\frac{2}{x}$图象上,点P是反比例函数y=$\frac{2}{x}$在第一象限图象上的一个动点,作点P关于原点对称的点P′,以P P′为边作等边△P P′C,点C(x,y)在第四象限.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com