
【题目】每年的3月15日是“国际消费者权益日”,许多家居商城都会利用这个契机进行打折促销活动.甲卖家的A商品成本为600元,在标价1000元的基础上打8折销售.
(1)现在甲卖家欲继续降价吸引买主,问最多降价多少元,才能使利润率不低于20%?
(2)据媒体爆料,有一些卖家先提高商品价格后再降价促销,存在欺诈行为.乙卖家也销售A商品,其成本、标价与甲卖家一致,以前每周可售出50件,现乙卖家先将标价提高2m%,再大幅降价24m元,使得A商品在3月15日那一天卖出的数量就比原来一周卖出的数量增加了 ![]() m%,这样一天的利润达到了20000元,求m的值.
m%,这样一天的利润达到了20000元,求m的值.
【答案】(1)最多降价80元, 才能使利润率不低于20%;(2)60.
【解析】
(1)设降价x元,则实际售价为”标价×折扣数-x“,然后根据题意列出不等式,解得x的取值范围,然后求出x的最大值即可;
(2)设m%=a(则m=100a),分别表示出降价后一件商品的利润和销售数量,然后利用“一件利润×销售数量=总利润”列出方程,解方程得m的值即可.
(1)设降价x元,
依题意,得:(1000×0.8-x)≥600×(1+20%),
解得:x≤80.
答:最多降价80元,才能使利润率不低于20%.
(2)设m%=a,依题意,得:[1000(1+2a)-2400a-600]50(1+![]() a)=20000,
a)=20000,
整理,得:5a2-3a=0,
解得:a1=0(舍去),a2=![]() ,
,
∴m%=![]() ,
,
∴m=60.
答:m的值为60.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
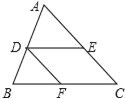
【题目】如图,在△ABC中,点D、E、F分别在边AB、AC、BC上,DE∥BC,DF∥AC,若△ADE与四边形DBCE的面积相等,则△DBF与△ADE的面积之比为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 3-2
D. 3-2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下,请补充完整.(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x | … | ﹣3 | ﹣ | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| m | ﹣1 | 0 | ﹣1 | 0 |
| 3 | … |
其中,m= .
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出两条函数的性质.
(4)进一步探究函数图象发现:
①函数图象与x轴有 个交点,所以对应的方程x2﹣2|x|=0有 个实数根;
②方程x2﹣2|x|=2有 个实数根.

③关于x的方程x2﹣2|x|=a有4个实数根时,a的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
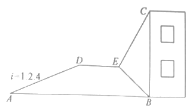
【题目】如图,小明利用所学数学知识测量某建筑物BC高度,采用了如下的方法:小明从与某建筑物底端B在同一水平线上的A点出发,先沿斜坡AD行走260米至坡顶D处,再从D处沿水平方向继续前行若干米后至点E处,在E点测得该建筑物顶端C的仰角为72°,建筑物底端B的俯角为63°,其中点A、B、C、D、E在同一平面内,斜坡AD的坡度i=1:2.4,根据小明的测量数据,计算得出建筑物BC的高度约为( )米(计算结果精DE确到0.1米,参考数据:sin72°≈0.95,tan72°≈3.08,sin63°≈0.89,tan63°≈1.96)
A.157.1 B.157.4 C.257.4 D.257.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,把抛物线在
,把抛物线在![]() 轴及其上方的部分记作
轴及其上方的部分记作![]() ,将
,将![]() 向右平移得
向右平移得![]() ,
,![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,若直线
,若直线![]() 与
与![]() ,
,![]() 共有
共有![]() 个不同的交点,则
个不同的交点,则![]() 的取值范围是________.
的取值范围是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
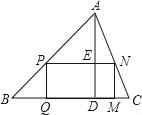
【题目】在△ABC中,AD是高,矩形PQMN的顶点P、N分别在AB、AC上,QM在边BC上,若BC=8cm,AD=6cm,且PN=2PQ,则矩形PQMN的周长为( )
A. 14.4cmB. 7.2cmC. 11.52cmD. 12.4cm
查看答案和解析>>
科目:初中数学 来源: 题型:
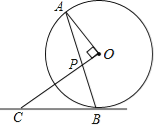
【题目】如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为![]() ,OP=1,求BC的长.
,OP=1,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
观察猜想

如图1,有公共直角顶点![]() 的两个不全等的等腰直角三角尺叠放在一起,点
的两个不全等的等腰直角三角尺叠放在一起,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上.
上.
(1)在图1中,你发现线段![]() ,
,![]() 的数量关系是___________,直线
的数量关系是___________,直线![]() ,
,![]() 的位置关系是________.
的位置关系是________.
操作发现
(2)将图1中的![]() 绕点
绕点![]() 逆时针旋转一个锐角得到图2,这时(1)中的两个结论是否成立?作出判断并说明理由;
逆时针旋转一个锐角得到图2,这时(1)中的两个结论是否成立?作出判断并说明理由;
拓广探索
(3)如图3,若只把“有公共直角顶点![]() 的两个不全等的等腰直角三角尺”改为“有公共顶角为
的两个不全等的等腰直角三角尺”改为“有公共顶角为![]() (锐角)的两个不全等等腰三角形”,
(锐角)的两个不全等等腰三角形”,![]() 绕点
绕点![]() 逆时针旋转任意一个锐角,这时(1)中的两个结论仍然成立吗?作出判断,不必说明理由.
逆时针旋转任意一个锐角,这时(1)中的两个结论仍然成立吗?作出判断,不必说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com