
【题目】如图,![]() 是△ABC的外接圆,
是△ABC的外接圆,![]() 于F,D为
于F,D为![]() 的中点,E是BA延长线上一点,
的中点,E是BA延长线上一点,![]() ,则∠CAD等于( )
,则∠CAD等于( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
由于D是弧AC的中点,可知∠ABC=2∠ACD;由于半径AO⊥BC,由垂径定理易证得AB=AC,即∠ACB=∠ABC=2∠ACD,由圆内接四边形的性质知:∠BCD=∠DAE=114°,由此可求出∠ACD的度数;而∠DAC和∠DCA是等弧所对的圆周角,则∠DAC=∠DCA,由此得解.
∵AO⊥BC,且AO是⊙O的半径,
∴AO垂直平分BC,
∴AB=AC,即∠ABC=∠ACB,
∵D是![]() 的中点,
的中点,
∴∠ABC=2∠DCA=2∠DAC,
∴∠ACB=2∠DCA,
∵四边形ABCD内接于⊙O,
∴∠BCD=∠DAE=114°,
∴∠ACB+∠DCA=114°,
即3∠DCA=114°,
∴∠CAD=∠DCA=38°.
故选:C.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】由于新冠肺炎影响,全国开展了“停课不停学”线上教学,为了解学生在家学习情况,五月7日开学后,某中学1200名学生参加了入学摸底测试,为了了解本次测试成绩情况,王老师从中抽取了部分学生的数学成绩(得分取整数,满分为100分)作为样本进行统计,并制作了如图频数分布表和频数分布直方图(不完整且局部污损,其中“■”表示被污损的数据).请解答下列问题:
成绩分组 | 频数 | 频率 |
50≤x<60 | 8 | 0.16 |
60≤x<70 | 12 | a |
70≤x<80 | ■ | 0.5 |
80≤x<90 | 3 | 0.06 |
90≤x≤100 | b | c |
合计 | ■ | 1 |
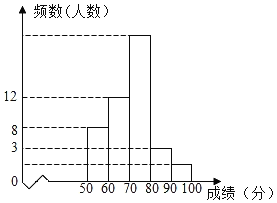
(1)写出a,b,c的值;
(2)请估计这1200名学生中有多少人的成绩不低于70分;
(3)在选取的样本中,从成绩是80分以上(含80分)的同学中随机抽取两名同学参加学习经验分享活动,求所抽取的2名同学来自同一组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天早上王文上学,先步行一段路,因时间紧,他又改乘出租车,结果到校时还是迟到了5分钟,其行程情况如图,若他出门时直接乘出租车(车速不变),则他( )
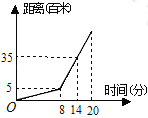
A.仍会迟到2分钟到校B.刚好按时到校
C.可以提前2分钟到校D.可以提前5分钟到校
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,PD切⊙O于点C,与BA的延长线交于点D,DE⊥PO交PO延长线于点E,连接PB,∠EDB=∠EPB.
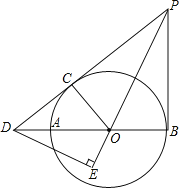
(1)求证:PB是的切线.
(2)若PB=6,DB=8,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有形状、大小和质地都完全相同的四张卡片A、B、C、D,正面上分别写有四个实数![]() 、
、![]() 、
、![]() 、
、![]() ,将这四张卡片背面朝上洗匀,从中随机抽取一张(不放回),接着再随机抽取一张.
,将这四张卡片背面朝上洗匀,从中随机抽取一张(不放回),接着再随机抽取一张.
(1)用画树形图或列表法表示抽取两张卡片可能出现的所有情况卡片(可用A、B、C、D表示);
(2)求抽到的两个数都是无理数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了全面了解某小区住户对物业的满意度情况,在小区内进行随机抽样调查,分为四个类别:A.非常满意;B.满意;C.基本满意;D.不满意.依据调查数据绘制成图1和图2的统计图(不完整).
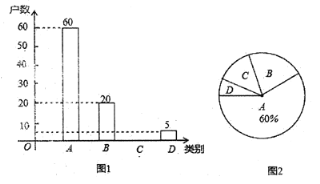
根据以上信息,解答下列问题:
(1)将图1补充完整;
(2)通过分析,住户对物业的满意度(A、B、C类视为满意)是 ;
(3)小区分为甲、乙两片住户区域,从甲区3户、乙区2户共5户中,随机抽取两户进行满意度回访,求这两户恰好都在同一住户区域的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
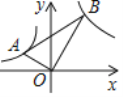
【题目】在平面直角坐标系中,将一块直角三角板如图放置,直角顶点与原点O重合,顶点A,B恰好分别落在函数![]() (x<0),y=
(x<0),y=![]() (x>0)的图象上,若sin∠BAO =
(x>0)的图象上,若sin∠BAO = ![]() ,则k的值为__________.
,则k的值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(2,3)。双曲线![]() 的图像经过BC的中点D,且与AB交于点E,连接DE。
的图像经过BC的中点D,且与AB交于点E,连接DE。

(1)求k的值及点E的坐标;
(2)若点F是边上一点,且△FBC∽△DEB,求直线FB的解析式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,港口A在观测站O的正东方向,OA=6km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )

A. 3![]() km B. 3
km B. 3![]() km C. 4km D. (3
km C. 4km D. (3![]() -3)km
-3)km
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com