
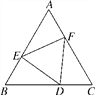
【题目】如图,在△ABC中,∠B=∠C,点D为BC边上(B,C点除外)的动点,∠EDF的两边与AB,AC分别交于点E,F,且BD=CF,BE=CD.
(1)求证:DE=DF;
(2)若∠EDF=m,用含m的代数式表示∠A的度数;
(3)连接EF,求当△DEF为等边三角形时∠A的度数.
【答案】(1)见解析;(2)180°-2m;(3)60°.
【解析】(1)利用SAS证明△BDE≌△CFD,再根据全等三角形的对应边相等即可得;
(2)由△BDE≌△CFD,可得∠BDE=∠CFD,再根据平角定义可得以及三角形内角和可得∠EDF=∠C,结合∠A+∠B+∠C=180°,∠B=∠C即可推得∠A=180°-2m;
(3)由△DEF为等边三角形,可得m=60°,继而可求得∠A=60°.
(1)在△BDE与△CFD中,
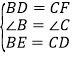 ,
,
∴△BDE≌△CFD,
∴DE=DF;
(2)∵△BDE≌△CFD,∴∠BDE=∠CFD,
∵∠BDE+∠EDF+∠CDF=180°,
∴∠EDF+∠CDF+∠CFD=180°,
∵∠C+∠CDF+∠CFD=180°,∴∠EDF=∠C,
∵∠A+∠B+∠C=180°,∠B=∠C,∴∠A+2∠EDF=180°,
∴∠A=180°-2∠EDF,即∠A=180°-2m;
(3)∵△DEF为等边三角形,∴m=60°,
∴∠A=180°-2×60°=60°.


科目:初中数学 来源: 题型:
【题目】为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等.经洽谈,甲商场的优惠方案是:每购买10套队服,送1个足球;乙商场的优惠方案是:若购买队服超过80套,则购买足球打八折.
(1)每套队服和每个足球的价格分别是多少?
(2)若城区四校联合购买100套队服和a个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所需的费用.
(3)假如你是本次购买任务的负责人,你认为到哪家商场购买比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CE是⊙O的直径,BD切⊙O于点D,DE∥BO,CE的延长线交BD于点A. 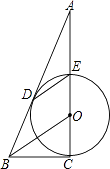
(1)求证:直线BC是⊙O的切线;
(2)若AE=2,tan∠DEO= ![]() ,求AO的长.
,求AO的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长等于( )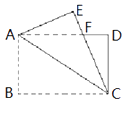
A. ![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知点A(0,8),B(6,0),点C(3,a)在线段AB上.
(1)则a的值为________;
(2)若点D(-4,3),求直线CD的函数表达式;
(3)点(-5,-4)在直线CD上吗?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
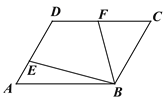
【题目】如图,□ABCD中,∠A=60°,点E、F分别在边AD、DC上,DE=DF,且∠EBF=60°,若AE=2,FC=3,则EF的长度为_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知直线 AB、CD 相交于点 O,∠COE=90°
(1)若∠AOC=36°,求∠BOE 的度数;
(2)若∠BOD:∠BOC=1:5,求∠AOE 的度数.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/13/1923292236627968/1924724835590144/STEM/dc8ee683cff64dfdb92368e07f9f9b9d.png]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】合作探究:你了解吗?骆驼被称为“沙漠之舟”,它的体温随时间的变化而发生较大的变化,观察图象回答下列问题: 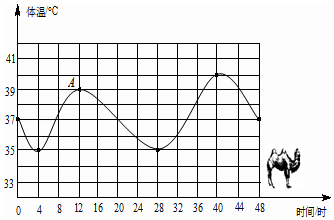
(1)一天中,骆驼的体温的变化范围是 , 它的体温从最低上升到最高需要时.
(2)从16时到24时,骆驼的体温下降了度.
(3)从时到时,骆驼的体温在上升,从时到时,从 时到时骆驼的体温在下降.
(4)你能看出第二天8时骆驼的体温与第一天8时的体温的关系是 .
(5)A点表示的是 , 还有时的温度与A点所表示的温度相同?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com