
 如图,直角三角形ABC中,AC=4,BC=3,P为斜边AB上一动点,且PE⊥AC,PF⊥BC,垂足分别是E、F,则线段EF长度的最小值是$\frac{12}{5}$.
如图,直角三角形ABC中,AC=4,BC=3,P为斜边AB上一动点,且PE⊥AC,PF⊥BC,垂足分别是E、F,则线段EF长度的最小值是$\frac{12}{5}$. 分析 先由矩形的判定定理推知四边形PECF是矩形;连接PC,则PC=EF,所以要使EF,即PC最短,只需PC⊥AB即可;然后根据三角形的等积转换即可求得PC的值.
解答 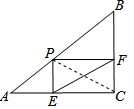 解:连接PC.
解:连接PC.
∵PE⊥AC,PF⊥BC,
∴∠PEC=∠PFC=∠C=90°;
又∵∠ACB=90°,
∴四边形ECFP是矩形,
∴EF=PC,
∴当PC最小时,EF也最小,
即当CP⊥AB时,PC最小,
∵AC=4,BC=3,
∴AB=5,
∴$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•PC,
∴PC=$\frac{12}{5}$.
∴线段EF长的最小值为$\frac{12}{5}$;
故答案为:$\frac{12}{5}$.
点评 本题考查了勾股定理、矩形的判定与性质、垂线段最短.利用“两点之间垂线段最短”找出PC⊥AB时,PC取最小值是解答此题的关键.


科目:初中数学 来源: 题型:填空题
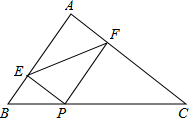 在△ABC中,AB=6cm,AC=8cm,BC=10cm,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,连接EF,则EF的最小值为$\frac{24}{5}$cm.
在△ABC中,AB=6cm,AC=8cm,BC=10cm,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,连接EF,则EF的最小值为$\frac{24}{5}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
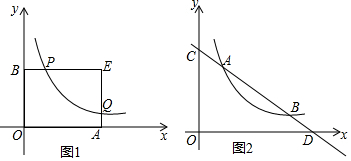
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | {x|a<x<$\frac{1}{a}$} | B. | {x|$\frac{1}{a}$<x<a} | C. | {x|x<a或x>$\frac{1}{a}$} | D. | {x|x<$\frac{1}{a}$或x>a} |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2a+b)(2a-b) | B. | (-2a+b)(b-2a) | C. | (-2a+b)(-2a-b) | D. | (2a-b)-(2a-b) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com