
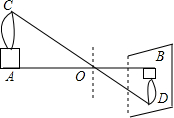
 如图,火焰的光线穿过小孔O,在竖直的屏幕上形成倒立的像,像的长度为2cm,OA=60cm,OB=15cm,求火焰的长度AC.
如图,火焰的光线穿过小孔O,在竖直的屏幕上形成倒立的像,像的长度为2cm,OA=60cm,OB=15cm,求火焰的长度AC. 分析 连接AC、BD,可证明△AOC∽△BOD,根据相似三角形的性质可得$\frac{AC}{DB}$=$\frac{AO}{BO}$,代入相应数据进行计算即可.
解答  解:连接AC、BD,
解:连接AC、BD,
∵CA⊥AB,DB⊥AB,
∴∠CAO=∠DBO=90°,
∵∠COA=∠DOB,
∴△AOC∽△BOD,
∴$\frac{AC}{DB}$=$\frac{AO}{BO}$,
∵BD=2cm,OA=60cm,OB=15cm,
∴$\frac{AC}{2}$=$\frac{60}{15}$,
解得:AC=8cm,
答:火焰AC的长度为8cm.
点评 此题主要考查了相似三角形的应用,关键是掌握相似三角形,对应边成比例.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,用下面的方法可以画△AOB的内接等边三角形,阅读后解答相应问题.
如图,用下面的方法可以画△AOB的内接等边三角形,阅读后解答相应问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
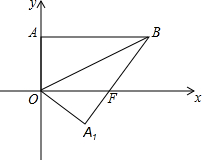 如图,平面直角坐标系中,点B的坐标为(4,2),过点B作y轴的垂线,垂足为A,连结OB,将△OAB沿OB折叠,使点A落在点A1处,A1B与x轴交与点F.
如图,平面直角坐标系中,点B的坐标为(4,2),过点B作y轴的垂线,垂足为A,连结OB,将△OAB沿OB折叠,使点A落在点A1处,A1B与x轴交与点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com