
如图,函数y1=k1x+b的图象与函数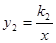 (x>0)的图象交于A、B两点,与y轴交于C点.已知A点的坐标为(2,1),C点的坐标为(0,3).
(x>0)的图象交于A、B两点,与y轴交于C点.已知A点的坐标为(2,1),C点的坐标为(0,3).
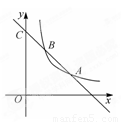
(1)求函数y1的表达式和B点坐标;
(2)观察图象,比较当x>0时,y1和y2的大小.
(1)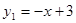 ,(2,1);(2)当
,(2,1);(2)当 或
或 时,
时, ,当
,当 或
或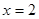 时,
时, ,当
,当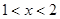 时,
时,
【解析】
试题分析:(1)把A点的坐标、C点的坐标代入y1=k1x+b即可求得函数y1的表达式,把A点的坐标代入函数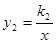 即可求得函数y2的表达式,再与函数y1的表达式组成方程组,即可求得B点坐标;
即可求得函数y2的表达式,再与函数y1的表达式组成方程组,即可求得B点坐标;
(2)仔细观察图象特征,以交点为界分情况讨论即可.
(1)∵y1=k1x+b的图象过点A(2,1),点C(0,3)
∴ ,解得
,解得
∴函数y1的表达式为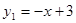
∵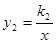 (x>0)的图象过点A(2,1)
(x>0)的图象过点A(2,1)
∴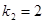
∴函数y2的表达式为
由 得
得 ,
,
∴B点坐标为(2,1);
(2)当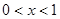 或
或 时,
时,
当 或
或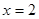 时,
时,
当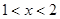 时,
时,
考点:待定系数法求函数关系式
点评:解题的关键是熟练掌握图象在上方的部分的函数值较大,图象在下方的部分的函数值较小.


科目:初中数学 来源:2011年湖北省恩施自治州中考数学试题 题型:013
一次函数y1=k1x+b和反比例函数y2=![]() (k1·k2≠0)的图象如图所示,若y1>y2,则x的取值范围是
(k1·k2≠0)的图象如图所示,若y1>y2,则x的取值范围是
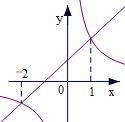
-2<x<0或x>1
-2<x<1
x<-2或x>1
x<-2或0<x<1
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,一次函数y1=k1x+2与反比例函数y2=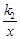 的图象交于点A (4,m)和B(-8,-2),与y轴交于点C
的图象交于点A (4,m)和B(-8,-2),与y轴交于点C
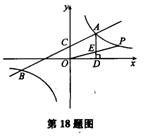
1.k1=_______,k2=______
2.根据函数图象可知,当y1>y2时,x的取值范围是______.
3.过点A作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E,当S四边形ODAC:S△CE=3:1时,求点P的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
 的图象交于点A (4,m)和B(-8,-2),与y轴交于点C
的图象交于点A (4,m)和B(-8,-2),与y轴交于点C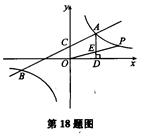
查看答案和解析>>
科目:初中数学 来源:2013届湖南省八年级反比例函数测试数学试卷(解析版) 题型:解答题
如图,一次函数y1=k1x+2与反比例函数y2= 的图象交于点A (4,m)和B(-8,-2),与y轴交于点C
的图象交于点A (4,m)和B(-8,-2),与y轴交于点C
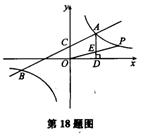
1.k1=_______,k2=______
2.根据函数图象可知,当y1>y2时,x的取值范围是______.
3.过点A作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E,当S四边形ODAC:S△CE=3:1时,求点P的坐标
查看答案和解析>>
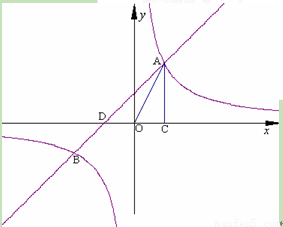
科目:初中数学 来源:2011年初中毕业升学考试(北京卷)数学解析版 题型:解答题
(2011山东烟台,22,8分)
如图,已知反比例函数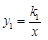 (k1>0)与一次函数
(k1>0)与一次函数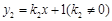 相交于A、B两点,AC⊥x轴于点C.
若△OAC的面积为1,且tan∠AOC=2 .
相交于A、B两点,AC⊥x轴于点C.
若△OAC的面积为1,且tan∠AOC=2 .
(1)求出反比例函数与一次函数的解析式;
(2)请直接写出B点的坐标,并指出当x为何值时,反比例函数y1的值大于一次函数y2的值?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com