
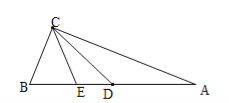
【题目】已知△ABC中,∠ACB=90°,CD、CE分别是中线和角平分线,当∠A= °时,△CDE是等腰三角形.
【答案】15或75.
【解析】
试题分析:有两种情况:①中线CD在角平分线CE的左边,由直角三角形斜边中线定理可以知道△BCD是等腰三角形,△CDE要是等腰三角形只有一种情况,即CE=DE,∠DCE=∠CDE,由外角定理可以知道∠CDE=∠B+∠BCD=2∠BCD,又因为∠CDE=∠DCE,且∠DCE+∠BCD=45°,所以3∠BCD=3∠B=45°,∠B=15°,∠A=90°-∠B=75°;

②中线CD在角平分线CE的右边,由直角三角形斜边中线定理可以知道△ACD是等腰三角形,△CDE要是等腰三角形只有一种情况,即CE=DE,∠DCE=∠CDE,由外角定理可以知道∠CDE=∠A+∠ACD=2∠ACD,又因为∠CDE=∠DCE,且∠DCE+∠ACD=45°,所以3∠ACD=3∠A=45°,∠A=15°;故答案为:15或75.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某地的一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1:1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1:![]() .
.
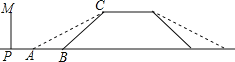
(1)求新坡面的坡角a;
(2)原天桥底部正前方8米处(PB的长)的文化墙PM是否需要拆桥?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种药品原价每盒25元,经过两次降价后每盒16元,两次降价的百分率相同,设每次降价的百分率为x,则符合题意的方程为( )
A. 16(1+2x)=25 B. 25(1﹣2x)=16 C. 16(1+x)2=25 D. 25(1﹣x)2=16
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com