
【题目】在直角坐标系中,有如图所示的Rt△ABO,AB⊥x轴于点B,斜边AO=10,sin∠AOB= ![]() ,反比例函数
,反比例函数 ![]() 的图象经过AO的中点C,且与AB交于点D,则点D的坐标为 .
的图象经过AO的中点C,且与AB交于点D,则点D的坐标为 . 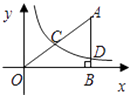
【答案】(8, ![]() )
)
【解析】解:∵斜边AO=10,sin∠AOB= ![]() ,
,
∴sin∠AOB= ![]() =
= ![]() ,
,
∴AB=6,
∴OB= ![]() =8,
=8,
∴A点坐标为(8,6),
而C点为OA的中点,
∴C点坐标为(4,3),
又∵反比例函数 ![]() 的图象经过点C,
的图象经过点C,
∴k=4×3=12,即反比例函数的解析式为y= ![]() ,
,
∵D点在反比例函数的图象上,且它的横坐标为8,
∴当x=8,y= ![]() =
= ![]() ,
,
所以D点坐标为(8, ![]() ).
).
所以答案是(8, ![]() ).
).
【考点精析】本题主要考查了反比例函数的性质的相关知识点,需要掌握性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大才能正确解答此题.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,点 O为数轴原点,点A表示的数是4,将线段OA沿数轴移动,移动后的线段记为O′A′.
(1)当点O′恰好是OA的中点时,数轴上点A′表示的数为 .
(2)设点A的移动距离AA′=x.
①当O′A=1时,求x的值;
②D为线段AA′的中点,点E在线段OO′上,且OE=![]() OO′,当点D,E所表示的数互为相反数时,求x的值.
OO′,当点D,E所表示的数互为相反数时,求x的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
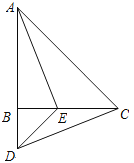
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC.
① 求证:△ABE≌△CBD;
② 若∠CAE=30°,求∠BDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列条件:①∠1=∠2,②∠3+∠4=180°,③∠5+∠6=180°,④∠2=∠3,⑤∠7=∠2+∠3,⑥∠7+∠4-∠1=180°中能判断直线![]() ∥
∥![]() 的有( )
的有( )
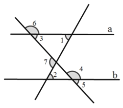
A. 3个 B. 4个 C. 5个 D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有足够多的长方形和正方形卡片,如下图: 
(1)如果选取1号、2号、3号卡片分别为1张、2张、3张,可拼成一个长方形(不重叠无缝隙),请画出这个长方形的草图,并运用拼图前后面积之间的关系说明这个长方形的代数意义. 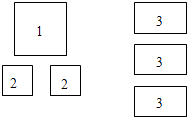
这个长方形的代数意义是 .
(2)小明想用类似方法解释多项式乘法(a+3b)(2a+b)=2a2+7ab+3b2 , 那么需用2号卡片张,3号卡片张.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC是一张等腰直角三角形纸板,∠C=90°,AC=BC=2, 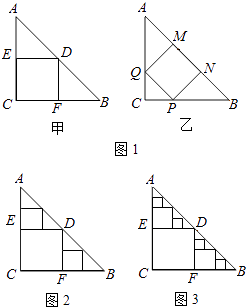
(1)要在这张纸板中剪出一个尽可能大的正方形,有甲、乙两种剪法(如图1),比较甲、乙两种剪法,哪种剪法所得的正方形面积大?请说明理由.
(2)图1中甲种剪法称为第1次剪取,记所得正方形面积为s1;按照甲种剪法,在余下的△ADE和△BDF中,分别剪取正方形,得到两个相同的正方形,称为第2次剪取,并记这两个正方形面积和为s2(如图2),则s2=;再在余下的四个三角形中,用同样方法分别剪取正方形,得到四个相同的正方形,称为第3次剪取,并记这四个正方形面积和为s3 , 继续操作下去…,则第10次剪取时,s10=;
(3)求第10次剪取后,余下的所有小三角形的面积之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=6cm,DE=2cm,则BC= . 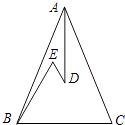
查看答案和解析>>
科目:初中数学 来源: 题型:
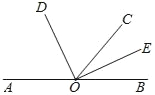
【题目】如图,点 A,O,B 在同一条直线上,OD,OE 分别平分∠AOC 和∠BOC.
(1)求∠DOE 的度数;
(2)如果∠COD=65°,求∠AOE 的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com