
【题目】过反比例函数 y= ![]() (k < 0)的图象上一点 A 作 x 轴的垂线交 x 轴于点 B ,O 为坐标原点, 且△ABO 的面积 S△ABO = 4 .
(k < 0)的图象上一点 A 作 x 轴的垂线交 x 轴于点 B ,O 为坐标原点, 且△ABO 的面积 S△ABO = 4 .
(1)求 k 的值;
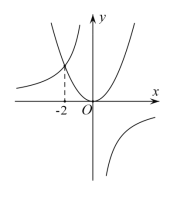
(2)若二次函数 y = ax2 与反比例函数 y= ![]() (k < 0)的图象交于点C(-2,m) ,请结合函数的图象写出满足 ax2<
(k < 0)的图象交于点C(-2,m) ,请结合函数的图象写出满足 ax2< ![]() 的x的取值范围.
的x的取值范围.
科目:初中数学 来源: 题型:
【题目】每个人都应怀有对水的敬畏之心,从点滴做起,节水、爱水,保护我们生活的美好世界.某地近年来持续干旱,为倡导节约用水,该地采用了“阶梯水价”计费方法,具体方法:每户每月用水量不超过4吨的每吨2元;超过4吨而不超过6吨的,超出4吨的部分每吨4元;超过6吨的,超出6吨的部分每吨6元.该地一家庭记录了去年12个月的月用水量如下表,下列关于用水量的统计量不会发生改变的是( )
用水量x(吨) | 3 | 4 | 5 | 6 | 7 |
频数 | 1 | 2 | 5 | 4﹣x | x |
A. 平均数、中位数 B. 众数、中位数 C. 平均数、方差 D. 众数、方差
查看答案和解析>>
科目:初中数学 来源: 题型:
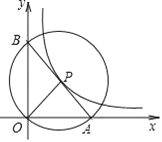
【题目】如图,在平面直角坐标系中,O 为坐标原点,P是反比例函数![]() 图象上任意一点,以P为圆心,PO为半径的圆与x轴交于点 A、与y轴交于点B,连接AB.
图象上任意一点,以P为圆心,PO为半径的圆与x轴交于点 A、与y轴交于点B,连接AB.
(1)求证:P为线段AB的中点;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,直径
中,直径![]() 垂直于弦
垂直于弦![]() ,垂足为
,垂足为![]() ,连结
,连结![]() ,将
,将![]() 沿
沿![]() 翻转得到
翻转得到![]() ,直线
,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() .
.

(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() 为
为![]() 的中点,
的中点,![]() ,求
,求![]() 的半径长;
的半径长;
(3)①求证:![]() ;
;
②若![]() 的面积为
的面积为![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种火爆的网红电子产品,每件产品成本![]() 元、工厂将该产品进行网络批发,批发单价
元、工厂将该产品进行网络批发,批发单价![]() (元)与一次性批发量
(元)与一次性批发量![]() (件)(
(件)(![]() 为正整数)之间满足如图所示的函数关系.
为正整数)之间满足如图所示的函数关系.
![]() 直接写出
直接写出![]() 与
与![]() 之间所满足的函数关系式,并写出自变量
之间所满足的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
![]() 若一次性批发量不超过
若一次性批发量不超过![]() 件,当批发量为多少件时,工厂获利最大?最大利润是多少?
件,当批发量为多少件时,工厂获利最大?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
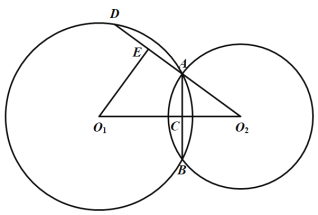
【题目】如图,⊙![]() 和⊙
和⊙![]() 相交于A、B两点,
相交于A、B两点,![]() 与AB交于点C,
与AB交于点C,![]() 的延长线交⊙
的延长线交⊙![]() 于点D,点E为AD的中点,AE=AC,联结
于点D,点E为AD的中点,AE=AC,联结![]() .
.
(1)求证:![]() ;
;
(2)如果![]() ,
,![]() ,求⊙
,求⊙![]() 的半径长.
的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 与y轴交于点C(0,2),它的顶点为D(1,m),且
与y轴交于点C(0,2),它的顶点为D(1,m),且![]() .
.
(1)求m的值及抛物线的表达式;
(2)将此抛物线向上平移后与x轴正半轴交于点A,与y轴交于点B,且OA=OB.若点A是由原抛物线上的点E平移所得,求点E的坐标;
(3)在(2)的条件下,点P是抛物线对称轴上的一点(位于x轴上方),且∠APB=45°.求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
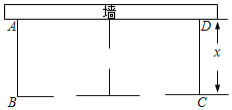
【题目】某农场要建一个饲养场(长方形![]() ,饲养场的一面靠墙(墙最大可用长度为27米),另三边用木栏围成,中间也用木栏隔开,分成两个场地,并在如图所示的三处各留1米宽的门(不用木栏),建成后木栏总长60米,设饲养场(长方形
,饲养场的一面靠墙(墙最大可用长度为27米),另三边用木栏围成,中间也用木栏隔开,分成两个场地,并在如图所示的三处各留1米宽的门(不用木栏),建成后木栏总长60米,设饲养场(长方形![]() 的宽为
的宽为![]() 米.
米.
(1)求饲养场的长![]() (用含
(用含![]() 的代数式表示).
的代数式表示).
(2)若饲养场的面积为![]() ,求
,求![]() 的值.
的值.
(3)当![]() 为何值时,饲养场的面积最大,此时饲养场达到的最大面积为多少
为何值时,饲养场的面积最大,此时饲养场达到的最大面积为多少![]() ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com