
【题目】为了认真贯彻教育部关于与开展“阳光体育”活动的文件精神,实施全国亿万学生每天集体锻炼一小时活动,吸引同学们走向操场、走进大自然、走到阳光下,积极参加体育锻炼,掀起校园内体育锻炼热潮,我市各学校结合实际情况举办了“阳光体育”系列活动,为了解“阳光体育”活动的落实情况,我市教育部门在红旗中学2000名学生中,随机抽取了若干名学生进行问卷调查(要求每位学生只能填写一种自己喜欢的活动),并将调查结果绘制成如下两幅不完整的统计图.

根据以上信息,解答下列问题:
(1)参加调查的人数共有 人,在扇形统计图中,表示“C”的扇形的圆心角为 度;
(2)补全条形统计图,并计算扇形统计图中m的值;
(3)若要从该校喜欢“D”项目的学生中随机选择8名进行节目排练,则喜欢该项目的小丽同学被选中的概率是多少
科目:初中数学 来源: 题型:
【题目】如图,OM是∠AOC的平分线,ON是∠BOC的平分线. 
(1)如图1,当∠AOB=90°,∠BOC=60°时,∠MON的度数是多少?为什么?
(2)如图2,当∠AOB=70°,∠BOC=60°时,∠MON= (直接写出结果)
(3)如图3,当∠AOB=α,∠BOC=β时,猜想:∠MON= (直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
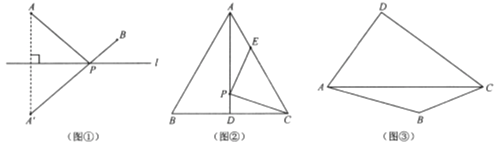
【题目】【新知理解】
如图①,若点![]() 、
、![]() 在直线l同侧,在直线l上找一点
在直线l同侧,在直线l上找一点![]() ,使
,使![]() 的值最小.
的值最小.
作法:作点![]() 关于直线l的对称点
关于直线l的对称点![]() ,连接
,连接![]() 交直线l于点
交直线l于点![]() ,则点
,则点![]() 即为所求.
即为所求.
【解决问题】
如图②,![]() 是边长为6cm的等边三角形
是边长为6cm的等边三角形![]() 的中线,点
的中线,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,则
上,则![]() 的最小值为 cm;
的最小值为 cm;
【拓展研究】
如图③,在四边形![]() 的对角线
的对角线![]() 上找一点
上找一点![]() ,使
,使![]() .(保留作图痕迹,并对作图方法进行说明)
.(保留作图痕迹,并对作图方法进行说明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴的原点为0,点A、B、C是数轴上的三点,点B对应的数位1,AB=6,BC=2,动点P、Q同时从A、C出发,分别以每秒2个长度单位和每秒1个长度单位的速度沿数轴正方向运动.设运动时间为t秒(t>0)
(1)求点A、C分别对应的数;
(2)求点P、Q分别对应的数(用含t的式子表示)
(3)试问当t为何值时,OP=OQ?![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB、BC、AC三边的长分别为![]() ,
, ![]() ,
, ![]() ,求这个三角形的面积.小明同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
,求这个三角形的面积.小明同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
(1)△ABC的面积为 .
(2)若△DEF的三边DE、EF、DF长分别为![]() ,
, ![]() ,
, ![]() ,请在图2的正方形网格中画出相应的△DEF,并求出△DEF的面积为 .
,请在图2的正方形网格中画出相应的△DEF,并求出△DEF的面积为 .
(3)在△ABC中,AB=2![]() ,AC=4,BC=2,以AB为边向△ABC外作△ABD(D与C在AB异侧),使△ABD为等腰直角三角形,则线段CD的长为 .
,AC=4,BC=2,以AB为边向△ABC外作△ABD(D与C在AB异侧),使△ABD为等腰直角三角形,则线段CD的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年宁波市中考新增英语口语听力自动化考试,考试需要耳麦,已知甲耳麦比乙耳麦贵20元,某校购买了甲耳麦40个、乙耳麦60个,共花费了6000元,假设甲耳麦每个x元,由题意得( )
A. 40x+60(x–20)=6000 B. 40x+60(x+20)=6000
C. 60x+40(x–20)=6000 D. 60x+40(x+20)=6000
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上三点M,O,N对应的数分别为﹣2,0,4,点P为数轴上任意一点,其对应的数为x.
(1)如果点P到点M、点N的距离相等,那么x的值是多少?
(2)数轴上是否存在点P,使点P到点M、点N的距离之和是7?如果存在,求出x的值;如果不存在,请说明理由;
(3)如果点P以每秒钟6个单位长度的速度从点O向右运动时,点M和点N分别以每秒钟1个单位长度和每秒钟3个单位长度的速度也向右运动,且三点同时出发,那么经过几秒钟,点P到点M、点N的距离相等.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com