
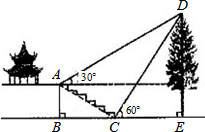
 如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为2m,台阶AC的坡度为1:$\sqrt{3}$,且B,C,E三点在同一条直线上.请根据以上条件求出树DE的高度(测倾器的高度忽略不计).
如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为2m,台阶AC的坡度为1:$\sqrt{3}$,且B,C,E三点在同一条直线上.请根据以上条件求出树DE的高度(测倾器的高度忽略不计). 分析 由于AF⊥AB,则四边形ABEF为矩形,设DE=x,在Rt△CDE中,CE═$\frac{DE}{tan∠DCE}$=$\frac{DE}{tan60°}$=$\frac{\sqrt{3}}{3}$x,在Rt△ABC中,得到$\frac{AB}{BC}$=$\frac{1}{\sqrt{3}}$,求出BC,在Rt△AFD中,求出AF,由AF=BC+CE即可求出x的长.
解答 解:∵AF⊥AB,AB⊥BE,DE⊥BE,
∴四边形ABEF为矩形,
∴AF=BE,EF=AB=2
设DE=x,在Rt△CDE中,CE=$\frac{DE}{tan∠DCE}$=$\frac{DE}{tan60°}$=$\frac{\sqrt{3}}{3}$x,
在Rt△ABC中,
∵$\frac{AB}{BC}$=$\frac{1}{\sqrt{3}}$,AB=2,
∴BC=2$\sqrt{3}$,
在Rt△AFD中,DF=DE-EF=x-2,
∴AF=$\frac{DF}{tan∠DAF}$=$\frac{x-2}{tan30°}$=$\sqrt{3}$(x-2),
∵AF=BE=BC+CE.
∴$\sqrt{3}$(x-2)=2$\sqrt{3}$+$\frac{\sqrt{3}}{3}$x,
解得x=6.
答:树DE的高度为6米.
点评 本题考查了解直角三角形的应用--仰角、坡度问题、矩形的判定与性质、三角函数;借助仰角构造直角三角形并解直角三角形是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
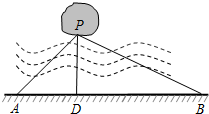 如图,宁波市共湖中有一小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PD,在小道上测得如下数据:AB=60米,∠PAB=45°,∠PBA=30°.请帮助小张求出小桥PD的长.($\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果精确到0.1米)
如图,宁波市共湖中有一小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PD,在小道上测得如下数据:AB=60米,∠PAB=45°,∠PBA=30°.请帮助小张求出小桥PD的长.($\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,一次函数y=kx+3分别与x,y轴交于点N,M,与反比例函数y=$\frac{3}{x}$(x>0)的图象交于点A,若AM:MN=2:3,则k=$\frac{10}{3}$.
如图,一次函数y=kx+3分别与x,y轴交于点N,M,与反比例函数y=$\frac{3}{x}$(x>0)的图象交于点A,若AM:MN=2:3,则k=$\frac{10}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
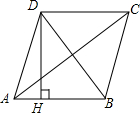 如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于( )
如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于( )| A. | $\frac{24}{5}$ | B. | $\frac{12}{5}$ | C. | 5 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com