
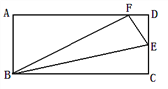
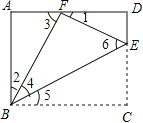
【题目】(本题9分)如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.
(1)求证:△ABF∽△DFE
(2)若△BEF也与△ABF相似,请求出![]() 的值 .
的值 .
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)在△ABF与△DFE中的对应角∠A=∠D=90°,∠2=∠1,易证△ABF∽△DFE;
(2)需要分类讨论:①△ABF∽△FBE;②△ABF∽△FEB时求出![]() 的值.
的值.
试题解析:(1)∵四边形ABCD是矩形,∴∠A=∠D=∠C=90°.
∵△BCE沿BE折叠为△BFE,∴∠BFE=∠C="90°." ∴∠AFB+∠DFE=180°﹣∠BFE=90°.
又∠AFB+∠ABF=90°,∴∠ABF=∠DFE。∴△ABE∽△DFE.
(2)①当△ABF∽△FBE时,∠2=∠4.
∵∠4=∠5,∠2+∠4+∠5=90°,∴∠2=∠4=∠5=30°.
∴设CE=EF=x,则BC=![]() x,DE=
x,DE=![]() x. ∴DC=
x. ∴DC=![]() x. ∴
x. ∴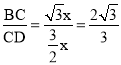 .
.
②当△ABF∽△FEB时,∠2=∠6,
∵∠4+∠6=90°,∴∠2+∠4=90°,这与∠2+∠4+∠5=90°相矛盾. ∴△ABF∽△FEB不成立.
综上所述, ![]() 的值是
的值是![]() .
.


科目:初中数学 来源: 题型:
【题目】一台机器原价60万元,如果每年的折旧率为x,两年后这台机器的价位为y万元,则y关于x的函数关系式为( )
A.y=60(1﹣x)2
B.y=60(1﹣x2)
C.y=60﹣x2
D.y=60(1+x)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD∥BC,∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P,作PE⊥AB于点E.若PE=2,则两平行线AD与BC间的距离为( ) 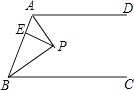
A.4
B.5
C.6
D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】联合国规定每年的6月5日是“世界环境日”,为配合今年的“世界环境日”宣传活动,某校课外活动小组对全校师生开展了以“爱护环境,从我做起”为主题的问卷调查活动,将调查结果分析整理后,制成了上面的两个统计图.
其中:A:能将垃圾放到规定的地方,而且还会考虑垃圾的分类;
B:能将垃圾放到规定的地方,但不会考虑垃圾的分类;
C:偶尔会将垃圾放到规定的地方;
D:随手乱扔垃圾.
根据以上信息回答下列问题:
(1)该校课外活动小组共调查了多少人?并补全上面的条形统计图;
(2)如果该校共有师生2400人,那么随手乱扔垃圾的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是等边△ABC内一点,OA=6,OB=8,OC=10,以B为旋转中心,将线段BO逆时针旋转60°得到线段BO′,连接AO′.则下列结论:①△BO′A可以由△BOC绕点B逆时针方向旋转60°得到;②连接OO′,则OO′=8;③∠AOB=150°;④ ![]() 其中正确的有( )
其中正确的有( )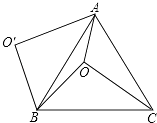
A.①②
B.①②③
C.①②④
D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com