
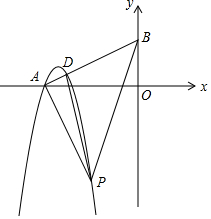
 已知抛物线C:y=(x+2)[t(x+1)-(x+3)],其中-7≤t≤-2,且无论t取任何符合条件的实数,点A,P都在抛物线C 上.
已知抛物线C:y=(x+2)[t(x+1)-(x+3)],其中-7≤t≤-2,且无论t取任何符合条件的实数,点A,P都在抛物线C 上.分析 (1)由条件求得抛物线解析式,即可求得其对称轴;
(2)把点代入抛物线解析式可得到n与t的关系式,由t的范围可求得n的取值范围,再与已知n的范围进行比较即可得出结论;
(3)过点P作PN⊥x轴于点N,可证得△PAN≌△ABO,可求得PA、OB的长,再证得△DAM∽△BAO,可用m表示出AD的长,则可表示出△PAD的面积,由A、B的坐标可求得直线AB的解析式,从而可用m表示出D点坐标,代入抛物线解析式可得到t与m的关系,利用t的范围可求得m的范围,再利用一次函数的性质可求得△PAD的最小值.
解答 解:
(1)当t=5时,y=-6x2-20x-16,
∵-$\frac{b}{2a}$=-$\frac{5}{3}$,
∴对称轴为x=-$\frac{5}{3}$;
(2)若(1,n)在抛物线上,将点(1,n)代入解析式,得n=6t-12,
∵-7≤t≤-2,
∴-54≤n≤-24,
∵-60≤n≤-30,
∴当-60≤n<-54时,点(1,n)不在抛物线C上;
当-54≤n≤-30时,点(1,n)在抛物线C上.
(3)由题得A(-2,0),P(-1,-2),
过点P作PN⊥x轴于点N,过D作DM⊥x轴于点M,
∴PN=AO=2,∠PNA=∠AOB=90°,
∵PA⊥AB,
∴∠PAN+∠BAO=90°,
又∵∠ABO+∠BAO=90°,
∴∠PAN=∠ABO,
在△PAN和△ABO中
$\left\{\begin{array}{l}{∠PAN=∠ABO}\\{∠PNA=∠AOB}\\{PN=AO}\end{array}\right.$
∴△PAN≌△ABO(AAS),
∴BO=AN=AO-NO=2-1=1,
∴PA=AB=$\sqrt{5}$,
∵∠DMA=∠BOA=90°,且∠DAM=∠BAO,
∴△DAM∽△BAO,
∴$\frac{AD}{AB}$=$\frac{DM}{BO}$,
∵点D的纵坐标为m+$\frac{1}{2}$,
∴AD=$\sqrt{5}$(m+$\frac{1}{2}$),
∴S△PAD=$\frac{1}{2}$ AP•AD=$\frac{1}{2}$×$\sqrt{5}$×$\sqrt{5}$(m+$\frac{1}{2}$)=$\frac{5}{2}$(m+$\frac{1}{2}$)=$\frac{5}{2}$m+$\frac{5}{4}$
∵A(-2,0),B(0,1),
∴直线AB的解析式为y=$\frac{1}{2}$x+1,当y=m+$\frac{1}{2}$时,x=2m-1,
∴D点坐标为(2m-1,m+$\frac{1}{2}$),代入抛物线C的解析式可得t=1+$\frac{5}{4m}$,
∵-7≤t≤-2,
∴-$\frac{5}{12}$≤m≤-$\frac{5}{32}$,且m+$\frac{1}{2}$>0,
∴S△PAD=$\frac{5}{2}$m+$\frac{5}{4}$,
∵$\frac{5}{2}$>0,
∴S△PAD随m的增大而增大,
∴当m取最小值-$\frac{5}{12}$时,S△PAD的最小值为$\frac{5}{24}$.
点评 本题为二次函数的综合应用,涉及待定系数法、二次函数的性质、全等三角形的判定和性质、相似三角形的判定和性质、一次函数的性质及方程思想等知识.在(1)中求出抛物线的解析式即可解决,在(2)中利用t与n的关系,求得点在抛物线上时n的范围是解题的关键,在(3)中通过构造三角形全等、相似,用m表示出AD的长,进一步表示出△PAD的面积是解题的关键.本题考查知识点较多,综合性较强,特别是最后一问难度较大.


科目:初中数学 来源: 题型:解答题
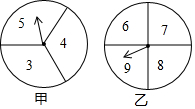 在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).
在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
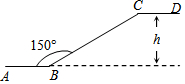 某商场一楼与二楼之间的手扶电梯如图所示.其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8m,则乘电梯从点B到点C上升的高度h是( )
某商场一楼与二楼之间的手扶电梯如图所示.其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8m,则乘电梯从点B到点C上升的高度h是( )| A. | 4$\sqrt{3}$m | B. | 8m | C. | $\frac{8}{3}$$\sqrt{3}$m | D. | 4m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
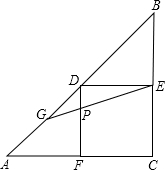 一节课上,数学老师在黑板上给出了这样一道题目:
一节课上,数学老师在黑板上给出了这样一道题目:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com