
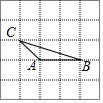
 如图,由25个同样大小的小正方形组成的正方形网格中,△ABC是格点三角形(每个顶点都是格点),在这个正方形网格中画另一个格点三角形,使得它与△ABC全等且仅有一条公共边,则符合要求的三角形共能画( )
如图,由25个同样大小的小正方形组成的正方形网格中,△ABC是格点三角形(每个顶点都是格点),在这个正方形网格中画另一个格点三角形,使得它与△ABC全等且仅有一条公共边,则符合要求的三角形共能画( )| A. | 5个 | B. | 6个 | C. | 7个 | D. | 8个 |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案科目:初中数学 来源: 题型:选择题
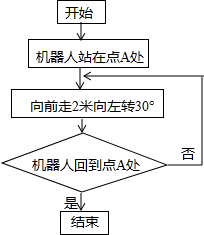 科技馆为某机器人编制一段程序,如果机器人在平地上按照图中所示的步骤行走,那么该机器人所走的总路程为( )
科技馆为某机器人编制一段程序,如果机器人在平地上按照图中所示的步骤行走,那么该机器人所走的总路程为( )| A. | 12米 | B. | 16米 | C. | 24米 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
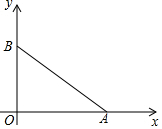 如图,在平面直角坐标系xOy中,已知点(4,0),B(0,3),若有一个直角三角形与Rt△ABO全等且有一条公共的直角边,试写出这个直角三角形未知顶点的坐标.
如图,在平面直角坐标系xOy中,已知点(4,0),B(0,3),若有一个直角三角形与Rt△ABO全等且有一条公共的直角边,试写出这个直角三角形未知顶点的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
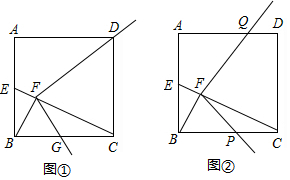
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com