
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
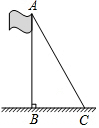 如图,为了测量旗杆AB的高度,可以利用从旗杆顶端垂下的绳子,当绳子垂直地面时,量得绳子比旗杆多1m,将绳子拉直到地面的C点,测得CB的长为5m,求旗杆AB的高度.
如图,为了测量旗杆AB的高度,可以利用从旗杆顶端垂下的绳子,当绳子垂直地面时,量得绳子比旗杆多1m,将绳子拉直到地面的C点,测得CB的长为5m,求旗杆AB的高度.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 甲 | 乙 | 丙 | 丁 | |
| 平均成绩(环) | 8.6 | 8.4 | 8.6 | 7.6 |
| 方差 | 0.94 | 0.74 | 0.56 | 1.92 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,将等腰直角三角形ABC绕点A逆时针旋转15°后得到△AB′C′,若AC=$\sqrt{3}$,则图中阴影部分的面积为$\frac{\sqrt{3}}{2}$.
如图,将等腰直角三角形ABC绕点A逆时针旋转15°后得到△AB′C′,若AC=$\sqrt{3}$,则图中阴影部分的面积为$\frac{\sqrt{3}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com