
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 先根据a、b、c为实数且满足$\sqrt{4-a}$+(b-$\sqrt{3}$)2+|c-$\sqrt{2}$|=0,求出a、b、c的值,然后代入a+c-b2-$\sqrt{2}$进行求解即可.
解答 解:∵a、b、c为实数且满足$\sqrt{4-a}$+(b-$\sqrt{3}$)2+|c-$\sqrt{2}$|=0,
∴a=4,b=$\sqrt{3}$,c=$\sqrt{2}$,
∴a+c-b2-$\sqrt{2}$
=4+$\sqrt{2}$-($\sqrt{3}$)2-$\sqrt{2}$
=4-3
=1.
故选B.
点评 本题考查了二次根式的化简求值,解答本题的关键在于根据a、b、c为实数且满足$\sqrt{4-a}$+(b-$\sqrt{3}$)2+|c-$\sqrt{2}$|=0,求出a、b、c的值.


科目:初中数学 来源: 题型:选择题
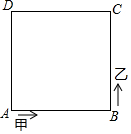 如图所示,甲、乙两人同时沿着边长为100m的正方形广场ABCD,按A→B→C→D→A…的顺序跑,甲从A出发,速度为82m/min,乙从B出发,速度为90m/min,则当乙第二次追到甲时,他在正方形广场的( )
如图所示,甲、乙两人同时沿着边长为100m的正方形广场ABCD,按A→B→C→D→A…的顺序跑,甲从A出发,速度为82m/min,乙从B出发,速度为90m/min,则当乙第二次追到甲时,他在正方形广场的( )| A. | AB边 | B. | BC边 | C. | CD边 | D. | AD边 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8、9、10、11、12 | B. | 8、9、11、12 | C. | 8、10、11、12 | D. | 8、11、12 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$x(x+1)=28 | B. | $\frac{1}{2}$x(x-1)=28 | C. | x(x+1)=28 | D. | x(x-1)=28 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com