
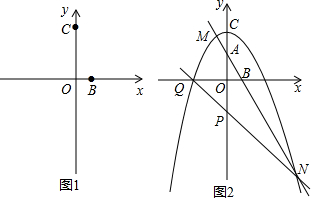
分析 (1)列方程组,把b看作常数,求方程组的解,写出点N和M的坐标;(
(2)如图2,作辅助线,构建平行线,证明△MDA∽△NEA,根据S△QAN=3S△QAM,由这两个三角形是不同底同高的两个三角形,其面积的比就是底边AN和AM的比,则EN=3MD,列式可得b的值;
(3)如图3,求Q的坐标为Q(-$\sqrt{2b}$,0),利用待定系数法求直线QN的解析式为:y=-x-$\sqrt{2b}$,分别表示PC和PN的长,列式可得结论.
解答 解:(1)由题意得:$\left\{\begin{array}{l}{y=-\frac{1}{2}{x}^{2}+b}\\{y=-2x+2}\end{array}\right.$,
-$\frac{1}{2}{x}^{2}$+b=-2x+2,
x2-4x+4=2b,
(x-2)2=2b,
x=2$±\sqrt{2b}$,
当x=2+$\sqrt{2b}$时,y=-2(2+$\sqrt{2b}$)+2=-2-2$\sqrt{2b}$,
当x=2-$\sqrt{2b}$时,y=-2(2-$\sqrt{2b}$)+2=-2+2$\sqrt{2b}$,
∵点M在点N的左侧,
∴M(2-$\sqrt{2b}$,-2+2$\sqrt{2b}$),N(2+$\sqrt{2b}$,-2-2$\sqrt{2b}$);
(2)如图2,过M作MD⊥y轴于D,过N作NE⊥y轴于E,
∴MD∥NE,
∴△MDA∽△NEA,
∴$\frac{MD}{EN}=\frac{AM}{AN}$,
∵S△QAN=3S△QAM,
∴$\frac{{S}_{△QAN}}{{S}_{△QAM}}$=$\frac{AN}{AM}$=3,
∴$\frac{MD}{EN}$=$\frac{1}{3}$,
∴EN=3MD,
即2+$\sqrt{2b}$=3($\sqrt{2b}$-2),
b=8;
(3)如图3,当y=0时,-$\frac{1}{2}{x}^{2}$+b=0,
x=$±\sqrt{2b}$,
∴Q(-$\sqrt{2b}$,0),
由(1)得:N(2+$\sqrt{2b}$,-2-2$\sqrt{2b}$),
当x=0时,y=b,
∴C(0,b),
设直线QN的解析式为:y=kx+a,
则$\left\{\begin{array}{l}{-\sqrt{2b}k+a=0}\\{(2+\sqrt{2b})k+a=-2-2\sqrt{2b}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{a=-\sqrt{2b}}\end{array}\right.$,
∴直线QN的解析式为:y=-x-$\sqrt{2b}$,
∴P(0,-$\sqrt{2b}$),
∴PC=b+$\sqrt{2b}$,
过N作NE⊥y轴于E,
在Rt△PEM中,PE=2+2$\sqrt{2b}$-$\sqrt{2b}$=2+$\sqrt{2b}$,
EN=2+$\sqrt{2b}$,
由勾股定理得:PN2=PE2+EN2,
∵PC=PN,
∴(b+$\sqrt{2b}$)2=2(2+$\sqrt{2b}$)2,
[$\sqrt{b}$($\sqrt{b}$+$\sqrt{2}$)]2=2[$\sqrt{2}$($\sqrt{2}$+$\sqrt{b}$)]2,
b=8.
点评 本题是二次函数的综合题,考查了利用待定系数法求函数的解析式、相似三角形的性质和判定、二次函数与两坐标轴的交点等知识,对于含字母系数的二次函数,计算时要注意把字母系数b看作常数,并与方程相结合,解决问题.


科目:初中数学 来源: 题型:解答题
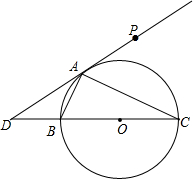 如图所示,Rt△ABC中,∠BAC=90°,∠C=30°,BC=2,⊙O是△ABC的外接圆,D是CB延长线上一点,且BD=1,连接DA,点P是射线DA上的动点.
如图所示,Rt△ABC中,∠BAC=90°,∠C=30°,BC=2,⊙O是△ABC的外接圆,D是CB延长线上一点,且BD=1,连接DA,点P是射线DA上的动点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
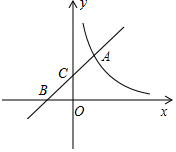 如图,直线y1=kx+2与反比例函数y2=$\frac{3}{x}$的图象交于点A(m,3),与坐标轴分别交于B,C两点.
如图,直线y1=kx+2与反比例函数y2=$\frac{3}{x}$的图象交于点A(m,3),与坐标轴分别交于B,C两点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 3 | C. | 6 | D. | 3$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线y=kx与双曲线y=$\frac{m-5}{x}$在第一象限交于点A,在第三象限交于点B,N是点A右侧双曲线上的动点,BN交x轴于M点.
如图,直线y=kx与双曲线y=$\frac{m-5}{x}$在第一象限交于点A,在第三象限交于点B,N是点A右侧双曲线上的动点,BN交x轴于M点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,抛物线y=-x2-2x+3与x轴交于A、C两点,与y轴交于点B,顶点为点D,已知点P(m,0)是线段CO上的动点,过点P作PQ⊥x轴交抛物线于点Q,交线段BC于点E,交直线CD于点F.
如图,在平面直角坐标系中,抛物线y=-x2-2x+3与x轴交于A、C两点,与y轴交于点B,顶点为点D,已知点P(m,0)是线段CO上的动点,过点P作PQ⊥x轴交抛物线于点Q,交线段BC于点E,交直线CD于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,七位同学正在玩丢手绢游戏:六人蹲在地上围成一个圆圈(假定圆圈的直径为6米,相邻两人距离相等),另有一人在圈外手持手绢绕着圆圈走,随意悄悄地将手绢放在某人身后….一次,小明将手绢丢给小杰身后,以2米/秒的速度行走;经过3秒后小杰发现,立刻拿起手绢以7米/秒的速度追赶小明,与此同时小明也加快了速度,其速度为5米/秒,问小杰能否在一圈内追上小明?
如图所示,七位同学正在玩丢手绢游戏:六人蹲在地上围成一个圆圈(假定圆圈的直径为6米,相邻两人距离相等),另有一人在圈外手持手绢绕着圆圈走,随意悄悄地将手绢放在某人身后….一次,小明将手绢丢给小杰身后,以2米/秒的速度行走;经过3秒后小杰发现,立刻拿起手绢以7米/秒的速度追赶小明,与此同时小明也加快了速度,其速度为5米/秒,问小杰能否在一圈内追上小明?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com