
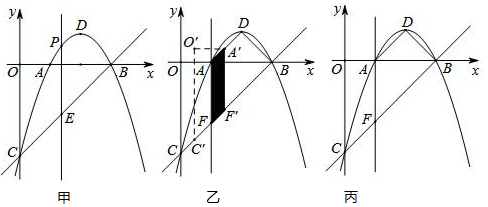
·ÖĪö £Ø1£©ĄūÓĆ“ż¶ØĻµŹż·Ø¼“æÉĒóµĆÅ×ĪļĻߵĽāĪöŹ½£¬Č»ŗó»ÆĪŖ¶„µćŹ½¼“æÉĒóµĆ¶„µćµÄ×ų±ź£®
£Ø2£©ĻČĒóµĆÖ±ĻßBCµÄ½āĪöŹ½£¬ÉčP£Øx£¬-x2+4x-3£©£¬ŌņF£Øx£¬x-3£©£¬øł¾ŻPFµČÓŚPµćµÄׯ×ų±ź¼õČ„FµćµÄׯ×ų±ź¼“æÉĒóµĆPF¹ŲÓŚxµÄŗÆŹż¹ŲĻµŹ½£¬“Ó¶ųĒóµĆPµÄ×ų±źŗĶPFµÄ×ī“óÖµ£»
£Ø3£©ŌŚŌĖ¶Æ¹ż³ĢÖŠ£¬·ÖČżÖÖĒéŠĪ£¬ŠčŅŖ·ÖĄąĢÖĀŪ£¬±ÜĆāĀ©½ā£®
½ā“š ½ā£ŗ£Ø1£©Å×ĪļĻߵĽāĪöŹ½£ŗy=-x2+4x-3£¬
”ąÓÉy=-x2+4x-3=-£Øx-2£©2+1£¬æÉÖŖ£ŗ¶„µćDµÄ×ų±ź£Ø2£¬1£©£®
£Ø2£©“ęŌŚ£®
ÉčÖ±ĻßBCµÄ½āĪöŹ½ĪŖ£ŗy=kx+b£¬
Ōņ$\left\{\begin{array}{l}{3k+b=0}\\{b=-3}\end{array}\right.$£¬½āµĆ$\left\{\begin{array}{l}{k=1}\\{b=-3}\end{array}\right.$£¬
”ąÖ±ĻßBCµÄ½āĪöŹ½ĪŖy=x-3£¬
ÉčP£Øx£¬-x2+4x-3£©£¬ŌņF£Øx£¬x-3£©£¬
”ąPF=£Ø-x2+4x-3£©-£Øx-3£©=-x2+3x=-£Øm-$\frac{3}{2}$£©2+$\frac{9}{4}$£¬
”ąµ±x=$\frac{3}{2}$Ź±£¬PEÓŠ×ī“óÖµĪŖ$\frac{9}{4}$£®
”ą“ęŌŚŅ»µćP£¬Ź¹Ļ߶ĪPEµÄ³¤×ī“ó£¬×ī“óÖµĪŖ$\frac{9}{4}$£®
£Ø3£©”ßA£Ø1£¬0£©”¢B£Ø3£¬0£©”¢D£Ø2£¬1£©”¢C£Ø0£¬-3£©£¬
”ąæÉĒóµĆÖ±ĻßADµÄ½āĪöŹ½ĪŖ£ŗy=x-1£»
Ö±ĻßBCµÄ½āĪöŹ½ĪŖ£ŗy=x-3£®
”ąAD”ĪBC£¬ĒŅÓėxÖįÕż°ėÖį¼Š½Ē¾łĪŖ45”ć£®
”ßAF”ĪyÖį£¬
”ąF£Ø1£¬-2£©£¬
”ąAF=2£®
¢Łµ±0”Üt”Ü$\sqrt{2}$Ź±£¬Čē“šĶ¼1-1ĖłŹ¾£®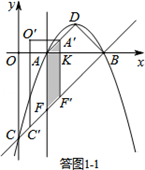
“ĖŹ±ĖıߊĪAFF”äA”äĪŖĘ½ŠŠĖıߊĪ£®
ÉčA”äF”äÓėxÖį½»ÓŚµćK£¬ŌņAK=$\frac{\sqrt{2}}{2}$AA”ä=$\frac{\sqrt{2}}{2}$t£®
”ąS=S?AFF”äA”ä=AF•AK=2”Į$\frac{\sqrt{2}}{2}$t=$\sqrt{2}$t£»
¢Śµ±$\sqrt{2}$£¼t”Ü2$\sqrt{2}$Ź±£¬Čē“šĶ¼1-2ĖłŹ¾£®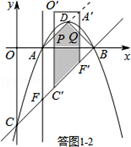
ÉčO”äC”äÓėAD½»ÓŚµćP£¬A”äF”äÓėBD½»ÓŚµćQ£¬
ŌņĖıߊĪPC”äF”äA”äĪŖĘ½ŠŠĖıߊĪ£¬”÷A”äDQĪŖµČŃüÖ±½ĒČż½ĒŠĪ£®
”ąS=S?PC”äF”äA”ä-S”÷A”äDQ=2”Į1-$\frac{1}{2}$£Øt-$\sqrt{2}$£©2=-$\frac{1}{2}$t2+$\sqrt{2}$t+1£»
¢Ūµ±2$\sqrt{2}$£¼t”Ü3$\sqrt{2}$Ź±£¬Čē“šĶ¼1-3ĖłŹ¾£®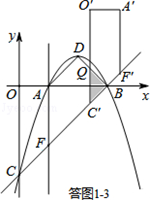
ÉčO”äC”äÓėBD½»ÓŚµćQ£¬Ōņ”÷BC”äQĪŖµČŃüÖ±½ĒČż½ĒŠĪ£®
”ßBC=3$\sqrt{2}$£¬CC”ä=t£¬
”ąBC”ä=3$\sqrt{2}$-t£®
”ąS=S”÷BC”äQ=$\frac{1}{2}$£Ø3$\sqrt{2}$-t£©2=$\frac{1}{2}$t2-3$\sqrt{2}$t+9£®
”ą×ŪÉĻĖłŹö£¬SÓėtµÄŗÆŹż¹ŲĻµŹ½ĪŖ£ŗ
S=$\left\{\begin{array}{l}{\sqrt{2}t£Ø0”Üt£¼\sqrt{2}£©}\\{-\frac{1}{2}{t}^{2}+\sqrt{2}t+1£Ø\sqrt{2}”Üt£¼2\sqrt{2}£©}\\{\frac{1}{2}{t}^{2}-3\sqrt{2}t+9£Ø2\sqrt{2}£¼t”Ü3\sqrt{2}£©}\end{array}\right.$£®
µćĘĄ ±¾ĢāŹĒ¶ž“ĪŗÆŹż×ŪŗĻĢā£¬æ¼²éĮĖ¶ž“ĪŗÆŹżµÄĶ¼ĻóÓėŠŌÖŹ”¢“ż¶ØĻµŹż·ØĒó½āĪöŹ½”¢×īÖµ”¢Ę½ŠŠĖıߊĪ”¢µČŃüÖ±½ĒČż½ĒŠĪ”¢Ķ¼ŠĪĆ껿¼ĘĖćµČÖŖŹ¶µć£®×¢Ņā·ÖĄąĢÖĀŪµÄŹżŃ§Ė¼Ļė¼°Ķ¼ŠĪĆ껿µÄ¼ĘĖć·½·Ø£®


 ½šŌæ³×ŹŌ¾ķĻµĮŠ“š°ø
½šŌæ³×ŹŌ¾ķĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
 ČēĶ¼£¬ABĪŖ”ŃOµÄÖ±¾¶£¬ĻŅBC£¬DEĻą½»ÓŚµćF£¬ĒŅDE”ĶABÓŚµćG£¬¹żµćC×÷”ŃOµÄĒŠĻß½»DEµÄŃÓ³¤ĻßÓŚµćH£®
ČēĶ¼£¬ABĪŖ”ŃOµÄÖ±¾¶£¬ĻŅBC£¬DEĻą½»ÓŚµćF£¬ĒŅDE”ĶABÓŚµćG£¬¹żµćC×÷”ŃOµÄĒŠĻß½»DEµÄŃÓ³¤ĻßÓŚµćH£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | $\frac{1}{24}$ | B£® | $\frac{1}{12}$ | C£® | $\frac{1}{6}$ | D£® | $\frac{1}{3}$ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® |  | B£® | 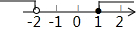 | C£® | 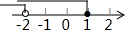 | D£® |  |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
 ČēĶ¼£¬ŌŚ¾ŲŠĪABCDÖŠ£¬µćE”¢F·Ö±šŌŚ±ßAB”¢BCÉĻ£¬ĒŅAE=$\frac{1}{3}$AB=2£¬½«¾ŲŠĪŃŲÖ±ĻßEFÕŪµž£¬µćBĒ”ŗĆĀäŌŚAD±ßÉĻµÄµćP“¦£¬Į¬½ÓBP½»EFÓŚµćQ£¬ĻĀĮŠ½įĀŪ£ŗ¢ŁEF=2BE£»¢Ś”÷APE”Õ”÷QEB£»¢ŪFQ=3EQ£»¢ÜSBFPE=8$\sqrt{3}$£¬ĘäÖŠÕżČ·µÄ½įĀŪŹĒ¢Ł¢Ś¢Ū£ØÖ»ĢīŠņŗÅ£©£®
ČēĶ¼£¬ŌŚ¾ŲŠĪABCDÖŠ£¬µćE”¢F·Ö±šŌŚ±ßAB”¢BCÉĻ£¬ĒŅAE=$\frac{1}{3}$AB=2£¬½«¾ŲŠĪŃŲÖ±ĻßEFÕŪµž£¬µćBĒ”ŗĆĀäŌŚAD±ßÉĻµÄµćP“¦£¬Į¬½ÓBP½»EFÓŚµćQ£¬ĻĀĮŠ½įĀŪ£ŗ¢ŁEF=2BE£»¢Ś”÷APE”Õ”÷QEB£»¢ŪFQ=3EQ£»¢ÜSBFPE=8$\sqrt{3}$£¬ĘäÖŠÕżČ·µÄ½įĀŪŹĒ¢Ł¢Ś¢Ū£ØÖ»ĢīŠņŗÅ£©£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
| ŌĀ¾łÓĆĖ®Įæ£Øt£© | µ„¼Ū£ØŌŖ/t£© |
| ²»³¬¹ż30£Øt£© | 3 |
| ³¬¹ż30t²»³¬¹ż45t | 5 |
| ³¬¹ż45t²æ·Ö | 7 |
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com