
【题目】抛物线y=x2+bx+c经过A(0,2),B(3,2)两点,若两动点D、E同时从原点O分别沿着x轴、y轴正方向运动,点E的速度是每秒1个单位长度,点D的速度是每秒2个单位长度.
(1)求抛物线与x轴的交点坐标;
(2)若点C为抛物线与x轴的交点,是否存在点D,使A、B、C、D四点围成的四边形是平行四边形?若存在,求点D的坐标;若不存在,说明理由;
(3)问几秒钟时,B、D、E在同一条直线上?
【答案】
(1)
解:抛物线y=x2+bx+c经过A(0,2),B(3,2)两点,
∴![]() ,
,
解得![]() ,
,
∴抛物线的解析式为:y=x2﹣3x+2,
令y=0,则x2﹣3x+2=0,
解得:x1=1,x2=2,
∴抛物线与x轴的交点坐标是(1,0),(2,0);
(2)
解:存在,由已知条件得AB∥x轴,
∴AB∥CD,
∴当AB=CD时,
以A、B、C、D四点围成的四边形是平行四边形,
设D(m,0),
当C(1,0)时,则CD=m﹣1,
∴m﹣1=3,
∴m=4,
当C(2,0)时,则CD=m﹣2,
∴m﹣2=3,
∴m=5,
∴D(5,0),
综上所述:当D(4,0)或(5,0)时,使A、B、C、D四点围成的四边形是平行四边形;
(3)
解:设t秒钟时,B、D、E在同一条直线上,则OE=t,OD=2t,
∴E(0,t),D(2t,0),
设直线BD的解析式为:y=kx+b,
∴,
解得k=﹣![]() 或k=
或k=![]() (不合题意舍去),
(不合题意舍去),
∴当k=﹣![]() ,t=
,t=![]() ,
,
∴点D、E运动![]() 秒钟时,B、D、E在同一条直线上.
秒钟时,B、D、E在同一条直线上.
【解析】(1)把A(0,2),B(3,2)两点代入抛物线y=x2+bx+c即可得到结果;
(2)存在,由已知条件得AB∥x轴,根据平行四边形的性质对边相等列方程即可求得结果;
(3)设t秒钟时,B、D、E在同一条直线上,则OE=t,OD=2t,设直线BD的解析式为:y=kx+b,把B,D,E三点代入,解方程组即可得到答案.


科目:初中数学 来源: 题型:
【题目】某市居民用电的电价实行阶梯收费,收费标准如下表:
一户居民每月用电量x(单位:度) | 电费价格(单位:元/度) |
0<x≤200 | a |
200<x≤400 | b |
x>400 | 0.92 |
(1)已知李叔家四月份用电286度,缴纳电费178.76元;五月份用电316度,缴纳电费198.56元,请你根据以上数据,求出表格中a,b的值.
(2)六月份是用电高峰期,李叔计划六月份电费支出不超过300元,那么李叔家六月份最多可用电多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴,y轴上,函数y=![]() 的图象过点P(4,3)和矩形的顶点B(m,n)(0<m<4).
的图象过点P(4,3)和矩形的顶点B(m,n)(0<m<4).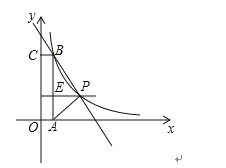
(1)求k的值.
(2)连接PA,PB,若△ABP的面积为6,求直线BP的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】11月读书节,深圳市为统计某学校初三学生读书状况,如下图:
(1)求三本以上的x值、参加调查的总人数,并补全统计图;
(2)三本以上的圆心角为 ° .
(3)全市有6.7万学生,三本以上有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 如图,△ABC是等腰三角形,AB=AC,请你用尺规作图将△ABC分成两个全等的三角形,并说明这两个三角形全等的理由.(保留作图痕迹,不写作法)
如图,△ABC是等腰三角形,AB=AC,请你用尺规作图将△ABC分成两个全等的三角形,并说明这两个三角形全等的理由.(保留作图痕迹,不写作法)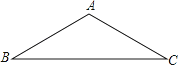
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,将直尺摆放在三角板上,使直尺与三角板的边分别交于点D,E,F,G,已知∠CGD=42°
(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)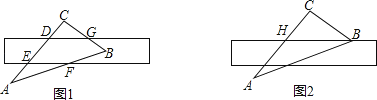
(1)求∠CEF的度数;
(2)将直尺向下平移,使直尺的边缘通过三角板的顶点B,交AC边于点H,如图②所示,点H,B在直尺上的读数分别为4,13.4,求BC的长(结果保留两位小数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com